
����˵���в���ȷ���ǣ� ��.
A�������н�ͨ�źŵƵ�·�ڣ��������������¼�
B��ij����ҽԺ���һ��������Ӥ����Ů���DZ�Ȼ�¼�
C��367����������2�����գ���������ͬ��ȷ���¼�
D�����ֱ�Ϊ3��5��9���������߶β���Χ��һ����������ȷ���¼�
B�� �������� ���������ֱ�Ӹ�������¼���ȷ���¼��Ķ�����⼴����ô𰸣�A�������н�ͨ�źŵƵ�·�ڣ��������������¼�������ȷ��B��ij����ҽԺ���һ��������Ӥ����Ů��������¼����ʴ���C��367����������2�����գ���������ͬ�DZ�Ȼ�¼�������ȷ���¼�������ȷ��D�����ֱ�Ϊ3��5��9���������߶β���Χ��һ���������Dz������¼�������ȷ���¼�������ȷ����ѡB��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����ʡ�������п���ѧ��ģ�Ծ� ���ͣ������
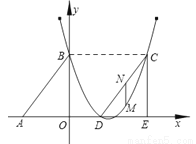
��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ(��3��0)��(0��4)��������y=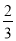 x2+bx+c������B���Ҷ�����ֱ��x=
x2+bx+c������B���Ҷ�����ֱ��x=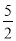 �ϣ�
�ϣ�
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2������DCE���ɡ�ABO��x������ƽ�Ƶõ��ģ����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ��ڸ��������ϣ���˵�����ɣ�
��3���ڣ�2����ǰ���£���M����CD����ֱ���·����������ϵ�һ�����㣬����M��MNƽ����y�ύCD�ڵ�N�����M�ĺ�����Ϊt��MN�ij���Ϊl����l��t֮��ĺ�����ϵʽ������lȡ���ֵʱ����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ����2017-2018ѧ�����꼶��һѧ����ѧ�ڶ����¿��Ծ� ���ͣ���ѡ��
��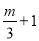 ��
�� ��Ϊ�෴������m��ֵΪ�� ��
��Ϊ�෴������m��ֵΪ�� ��
A. 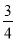 B.
B. 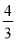 C.
C. 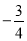 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������н�����2017����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ���ڵȱ�������ABC�У�AB=6��D��BC��һ�㣬��BC=3BD����ABD�Ƶ�A��ת��õ���ACE����CE�ij���Ϊ_____��
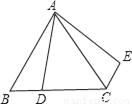
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������н�����2017����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ı���PAOB������OMN���ڽӾ��Σ�����P��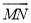 �ϣ��Ҳ���M��N�غϣ���P����
�ϣ��Ҳ���M��N�غϣ���P���� ���ƶ�ʱ������PAOB����״����С��֮�仯����AB�ij��ȣ� ��
���ƶ�ʱ������PAOB����״����С��֮�仯����AB�ij��ȣ� ��
A. ��� B. ��С C. ���� D. ����ȷ��
C �������������������PAOB������OMN���ڽӾ��Σ� ��AB=OP=�뾶�� ��P�������ƶ�ʱ���뾶һ��������AB���Ȳ��䣬 ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ����в��� ���ͣ������
ij����ͨ��˾�ֻ������շ���A�ײ�(�����15Ԫ,ͨ����ÿ����0.1Ԫ)��B�ײ�(�����0Ԫ,ͨ����ÿ����0.15Ԫ)����.��A�ײ�ÿ�»���Ϊy1(Ԫ),B�ײ�ÿ�»���Ϊy2(Ԫ),��ͨ��ʱ��Ϊx����.
(1)�ֱ��ʾ��y1��x,y2��x�ĺ�����ϵʽ.
(2)��ͨ��ʱ��Ϊ�ʱ,A,B�����ײ��շ�һ��?
(3)ʲô�����A�ײ�ʡǮ?
(1) y1=0.1x+15; y2=0.15x��(2)300��(3) ����ͨ��ʱ�����300����ʱ,A�ײ�ʡǮ. �������������������1������A�ײ͵��շ�Ϊ������ϻ��ѣ�B�ײ͵��շ�Ϊ������ʽ���ɣ���2�����������շ���ͬ�г����̣���⼴�ɣ���3�����ݣ�2���ļ�������С���շ���ͬʱ��ʱ��ѡ��B�ײͣ������շ���ͬ��ʱ��ѡ��A�� ����������������� ��1��A�ײ͵��շѷ�ʽ��y1=0��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ����в��� ���ͣ������
��֪��P��3����1������y��ĶԳƵ�Q�������ǣ�a+b��1��b������ab��ֵΪ________��
25 ��������������������ݹ���y��ԳƵ�������ص㣺�����껥Ϊ�෴���������겻���ֱ�ӵõ��𰸣� �ߵ�P��3��-1������y��ĶԳƵ�Q�������ǣ�a+b��1-b���� �࣬ ��ã� �� ��ab��ֵΪ��-5��2=-10���鿴�𰸺ͽ���>>
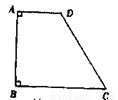
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ�. ���ͣ������
��֪����ͼ���ı���ABCD�У���A=��B=90�㣬��C=60�㣬CD=2AD,AB=4.
��1����AB����������P,ʹPC+PD��С��
��2�������1����PC+PD����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����������2017-2018ѧ����ѧ�ڳ��а��꼶���п�����ѧ�Ծ� ���ͣ������
����ʽ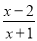 ��ֵΪ0����x��ֵΪ___________.
��ֵΪ0����x��ֵΪ___________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com