
车辆经过润扬大桥收费站时,4个收费通道 A.B、C、D中,可随机选择其中的一个通过.
(1)一辆车经过此收费站时,选择 A通道通过的概率是 ;
(2)求两辆车经过此收费站时,选择不同通道通过的概率.
(1);(2). 【解析】试题分析:(1)根据概率公式即可得到结论; (2)画出树状图即可得到结论. 试题解析:(1)选择 A通道通过的概率=, 故答案为: ; (2)设两辆车为甲,乙,如图,两辆车经过此收费站时,会有16种可能的结果,其中选择不同通道通过的有12种结果,∴选择不同通道通过的概率==. 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:填空题
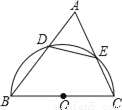
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC于D,E两点,且cosA=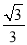 ,则S△ADE:S四边形DBCE的值为_____.
,则S△ADE:S四边形DBCE的值为_____.
查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
(1)甲的平均攀登速度是12米/分钟;(2)倍. 【解析】试题分析:(1)根据题意可以列出相应的分式方程,从而可以求得甲的平均攀登速度; (2)根据(1)中甲的速度可以表示出丙的速度,再用甲的速度比丙的平均攀登速度即可解答本题. 试题解析::(1)设乙的速度为x米/分钟, , 解得,x=10, 经检验,x=10是原分式方程的解, ∴1.2x=12, ...查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:单选题
下列各式能用平方差公式分解因式的有( )
①x2+y2;②x2-y2;③-x2-y2;④-x2+y2;⑤-x2+2xy-y2.
A. 1个B、2个C、3个D、4个
B 【解析】试题解析:能用平方差公式分解因式的有;②x2-y2;④-x2+y2;,共2个, 故选B.查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
如图,直线 :
:  与
与 轴、
轴、 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线 与
与 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥ 轴交
轴交 于点D,PE∥
于点D,PE∥ 轴交
轴交 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:填空题
如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为____________.
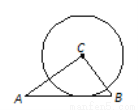
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:单选题
将二次函数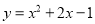 的图象沿
的图象沿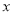 轴向右平移2个单位长度,得到的函数表达式是( )
轴向右平移2个单位长度,得到的函数表达式是( )
A. 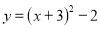 B.
B. 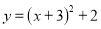 C.
C. 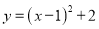 D.
D. 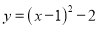
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:填空题
如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的关系是S1 S2(填“>”或“<”或“=”)

查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:填空题
已知某正数的两个平方根分别是m+4和2m﹣16,则这个正数的立方根为_____________.
4 【解析】试题解析:∵某正数的两个平方根分别是m+4和2m-16, 可得:m+4+2m-16=0, 解得:m=4, ∴这个正数的平方根为8和-8. ∴这个正确为64. ∴.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com