练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动. 

    (1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米? 

    (2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)

    （1）甲的平均攀登速度是12米/分钟；（2）倍. 【解析】试题分析：（1）根据题意可以列出相应的分式方程，从而可以求得甲的平均攀登速度； （2）根据（1）中甲的速度可以表示出丙的速度，再用甲的速度比丙的平均攀登速度即可解答本题． 试题解析：：（1）设乙的速度为x米/分钟， ， 解得，x=10， 经检验，x=10是原分式方程的解， ∴1.2x=12， ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：解答题

    阅读下列材料，完成相应学习任务：

    四点共圆的条件

    我们知道，过任意一个三角形的三个顶点能作一个圆，过任意一个四边形的四个顶点能作一个圆吗？小明经过实践探究发现：过对角互补的四边形的四个顶点能作一个圆，下面是小明运用反证法证明上述命题的过程：

    已知：在四边形ABCD中，∠B+∠D=180°．

    求证：过点A、B、C、D可作一个圆．

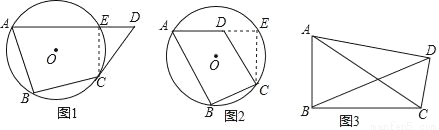
    证明：如图（1），假设过点A、B、C、D四点不能作一个圆，过A、B、C三点作圆，若点D在圆外，设AD与圆相交于点E，连接CE，则∠B+∠AEC=180°，而已知∠B+∠D=180°，所以∠AEC=∠D，而∠AEC是△CED的外角，∠AEC＞∠D，出现矛盾，故假设不成立，因此点D在过A、B、C三点的圆上．

    如图（2）假设过点A、B、C、D四点不能作一个圆，过A、B、C三点作圆，若点D在圆内，设AD的延长线与圆相交于点E，连接CE，则∠B+∠AEC=180°，而已知∠B+∠ADC=180°，所以∠AEC=∠ADC，而∠ADC是△CED的外角，∠ADC＞∠AEC，出现矛盾，故假设不成立，因此点D在过A、B、C三点的圆上．

    因此得到四点共圆的条件：过对角互补的四边形的四个顶点能作一个圆．

    学习任务：

    （1）材料中划线部分结论的依据是　 　．

    （2）证明过程中主要体现了下列哪种数学思想：　 　（填字母代号即可）

    A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想

    （3）如图（3），在四边形ABCD中，∠ABC=∠ADC=90°，∠CAD=16°．AD=BD，则求∠ADB的大小．

    （1）圆的内接四边形对角互补（2）D；（3）∠ADB=32° 【解析】试题分析：（1）材料中划线部分结论的依据圆的内接四边形对角互补； （2）证明过程中分点D在圆外或圆内两种情形讨论，主要体现了分类讨论的数学思想； （3）利用“对角互补的四边形的四个顶点能作一个圆”这个结论，结合同弧所对的圆周角相等以及等腰三角形的性质，即可解决问题． 试题解析： 【解析】 （1）材...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县九年级（上）期末数学试卷（五四学制） 题型：单选题

    下列说法错误的是（　 　）

    A. 直径是圆中最长的弦 B. 长度相等的两条弧是等弧

    C. 面积相等的两个圆是等圆 D. 半径相等的两个半圆是等弧

    B 【解析】试题解析：A、直径是圆中最长的弦，所以A选项的说法正确； B、在同圆或等圆中，长度相等的两条弧是等弧，所以B选项的说法错误； C、面积相等的两个圆的半径相等，则它们是等圆，所以C选项的说法正确； D、半径相等的两个半圆是等弧，所以D选项的说法正确． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：填空题

    开学整理教室时，老师总是先把每一列最前和最后的课桌摆好，然后再依次摆中间的课桌，一会儿一列课桌摆在一条线上，整整齐齐，这是因为_____．

    两点确定一条直线． 【解析】试题分析：根据两点确定一条直线． 故答案为：两点确定一条直线．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：单选题

    如图，将一张长方形纸片对折，然后剪下一个角，如果剪出的角展开后是一个直角，那么剪口线与折痕AB形成的夹角度数是(　　)

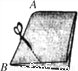
    A. 180° B. 90° C. 45° D. 22.5°

    C 【解析】试题分析：根据折叠图形的性质可知：剪口线与折痕AB形成的夹角的度数=90°÷2=45°，故选择C．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：解答题

    （1）分解因式：① 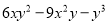， ②；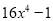

    （2）已知a+b=2,求的值.

    (1)①-y（3x-y）2; ②(4x2+1)(2x+1)(2x-1) (2) . 【解析】试题分析：（1）①先提取公因式-y，再对余下的多项式利用完全平方公式继续分解． ②两次运用平方差公式进行分解即可； （2）先化简题目中的式子，然后将a+b的值代入化简后的式子即可解答本题． 试题解析：（1）①6xy2-9x2y-y3 =-y（y2-6xy+9x2） =-y...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：单选题

    如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是(     )

    A. AD=AE B. DB=AE C. DF=EF D. DB=EC

    B 【解析】试题解析：∵△ABE≌△ACD， ∴AB=AC，AD=AE，∠B=∠C，故A正确； ∴AB-AD=AC-AE，即BD=EC，故D正确； 在△BDF和△CEF中 ∴△BDF≌△CEF（ASA）， ∴DF=EF，故C正确； 故选B．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    车辆经过润扬大桥收费站时，4个收费通道 A．B、C、D中，可随机选择其中的一个通过．

    （1）一辆车经过此收费站时，选择 A通道通过的概率是 ；

    （2）求两辆车经过此收费站时，选择不同通道通过的概率．

    （1）；（2）． 【解析】试题分析：（1）根据概率公式即可得到结论； （2）画出树状图即可得到结论． 试题解析：（1）选择 A通道通过的概率=， 故答案为： ； （2）设两辆车为甲，乙，如图，两辆车经过此收费站时，会有16种可能的结果，其中选择不同通道通过的有12种结果，∴选择不同通道通过的概率==．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：单选题

    不能判定四边形ABCD为平行四边形的题设是（　　）

    A. AB=CD，AB∥CD B. ∠A=∠C，∠B=∠D

    C. AB=AD，BC=CD D. AB=CD，AD=BC

    C 【解析】A.∵AB=CD，AB∥CD， ∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)；股本选项能判定四边形ABCD为平行四边形； B.∵∠A=∠C，∠B=∠D， ∴四边形ABCD为平行四边形(两组对角分别相等的四边形是平行四边形)；股本选项能判定四边形ABCD为平行四边形； C. 由AB=AD，BC=CD，不能判定四边形ABCD为平行...

    查看答案和解析>>

    同步练习册答案