
下列说法正确的有( )个.①a的相反数是-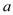 ;②所有的有理数都能用数轴上的点表示, ③m的绝对值是m,④若有理数a+b=0,则a,b互为相反数,⑤绝对值等于它相反数的是0和-1.
;②所有的有理数都能用数轴上的点表示, ③m的绝对值是m,④若有理数a+b=0,则a,b互为相反数,⑤绝对值等于它相反数的是0和-1.
A. 2 B. 3 C. 4 D. 5
B 【解析】①a的相反数是-a,正确; ②所有的有理数都能用数轴上的点表示, 正确; ③m的绝对值是m,错误; ④若有理数a+b=0,则a,b互为相反数,正确; ⑤绝对值等于它相反数的是0和负数,故错误. 故说法正确的有3个. 故选:B.科目:初中数学 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:单选题
下列函数中,二次函数的是
A. y=2x2+1 B. y=2x+1 C. y=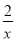 D. y=x2-(x-1)2
D. y=x2-(x-1)2
查看答案和解析>>
科目:初中数学 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:单选题
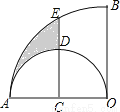
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交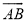 于点E,以点C为圆心,OA的长为直径作半圆交CE于点D.若OA=4,则图中阴影部分的面积为( )
于点E,以点C为圆心,OA的长为直径作半圆交CE于点D.若OA=4,则图中阴影部分的面积为( )
A. 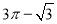 B.
B. 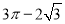 C.
C. 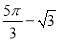 D.
D. 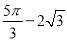
查看答案和解析>>
科目:初中数学 来源:山东省淄博市2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
若a<0,b<0,则a-(-b)一定是__________(填负数,0或正数).
负数. 【解析】由于a<0,b<0,然后根据有理数减法法则即可判定a-(-b)是正数还是负数. ∵a<0,b<0, 而a-(-b)=a+b, ∴a-(-b)一定是 负数.查看答案和解析>>
科目:初中数学 来源:山东省淄博市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
下列计算:①0-(-5)=-5;② (-3)+(-9)=-12;③ 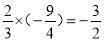 ;④(-36)÷(-9)=-4.其中正确的个数是( ).
;④(-36)÷(-9)=-4.其中正确的个数是( ).
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】①0?(?5)=5,错误; ②(?3)+(?9)=?12,正确; ③③×(?)=?,正确; ④(?36)÷(?9)=4,错误. 故选:B.查看答案和解析>>
科目:初中数学 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
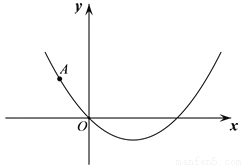
在平面直角坐标系xOy中,抛物线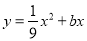 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作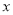 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在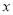 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.
查看答案和解析>>
科目:初中数学 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
已知二次函数y=x2-4x+3.
(1)在网格中,画出该函数的图象.
(2)(1)中图象与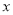 轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:单选题
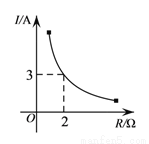
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A. 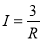 B.
B. 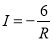 C.
C. 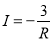 D.
D. 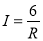
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
先化简,再求值: 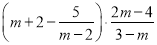 ,其中
,其中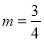 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com