
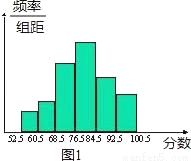
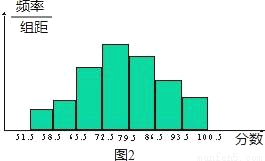
在一次环保知识测试中,三年一班的两名同学根据班级成绩(分数为整数)分别绘制了不同的频率分布直方图,如图1、2,已知图1从左到右每个小组的频率分别为0.04、0.08、0.24、0.32、0.20、0.12,其中68.5~76.5小组的频数为12;图2从左到右每个小组的频数之比为1:2:4:7:6:3:2,请结合条件和频率分布直方图回答下列问题:
(1)三年一班参加测试的人数是多少?
(2)若这次测试的成绩80分以上(含80分)为优秀,则优秀率是多少?
(3)若这次测试的成绩60分以上(含60分)为及格,则及格率是多少?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
2014年3月14日,“玉兔号”月球车成功在距地球约384400公里远的月球上自主唤醒,将384400这个数用科学记数法表示为_____.
3.844×105 【解析】384400=3.844×105.查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:解答题
关于的一元二次方程x2+2x+k+1=0的有两个实数解是x1和x2.
(1)求k的取值范围;
(2)如果x1+x2-x1x2<-1且k为整数,求k的值.
(1)k≤0;(2)k的值为-1和0. 【解析】试题分析:(1)∵方程有实数根 ∴⊿=22-4k+1)≥0解得 k≤0. (2)根据一元二次方程根与系数的关系,得x1+x2=-2, x1x2=k+1 得 -2—( k+1)<-1 解得 k>-2 ∴ -2<k≤0 ∵k为整数 ∴k的值为-1和0. 试题解析:【解析】 ∵(1)方程有实数根 ∴⊿=22-4k+1)≥0....查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:单选题
使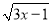 有意义的x的取值范围是( )
有意义的x的取值范围是( )
A. x>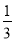 B. x>-
B. x>-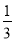 C. x≥
C. x≥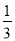 D. x≥-
D. x≥-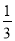
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:解答题
如图,在等腰△ABC中,AB=AC=5,BC=6,点D为BC边上一动点(不与点B重合),过D作射线DE交AB边于E,使∠BDE=∠A,以D为圆心、DC的长为半径作⊙D.
(1)设BD=x,AE=y,求y关于x的函数关系式,并写出定义域.
(2)当⊙D与AB边相切时,求BD的长.
(3)如果⊙E是以E为圆心,AE的长为半径的圆,那么当BD的长为多少时,⊙D与⊙E相切?
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:填空题
(3分)如图,已知Rt△ABC中,∠C=90°,AC=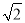 ,BC=1,若以C为圆心,CB为半径的圆交AB于点P,则AP=_____.
,BC=1,若以C为圆心,CB为半径的圆交AB于点P,则AP=_____.
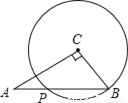
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:单选题
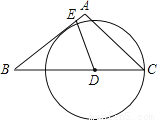
如图,四边形ABCD为圆内接四边形,E为DA延长线上一点,若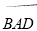 的度数为70°,则∠BAE的度数为( )
的度数为70°,则∠BAE的度数为( )
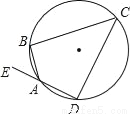
A. 140° B. 70° C. 35° D. 20°
C 【解析】试题解析:∵的度数为 故选C.查看答案和解析>>
科目:初中数学 来源:2017年天津109中中考数学模拟试卷 题型:填空题
如图在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB,CA′相交于点D,则线段BD的长为___________.
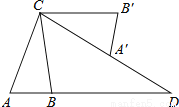
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
已知二次函数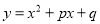 图象的顶点
图象的顶点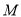 为直线
为直线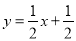 与
与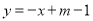 的交点.
的交点.
(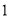 )用含
)用含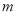 的代数式来表示顶点
的代数式来表示顶点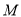 的坐标.
的坐标.
( )当
)当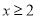 时,二次函数
时,二次函数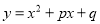 与
与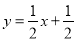 的值均随
的值均随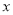 的增大而增大,求
的增大而增大,求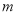 的取值范围.
的取值范围.
(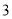 )若
)若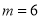 ,当
,当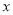 取值为
取值为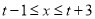 时,二次函数
时,二次函数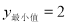 ,求
,求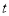 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com