
如图,过原点O的直线与反比例函数y1 , y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=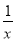 ,则y2与x的函数表达式是________ .
,则y2与x的函数表达式是________ .
科目:初中数学 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:单选题
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
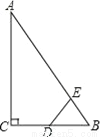
A. 2 B. 2.5或3.5 C. 3.5或4.5 D. 2或3.5或4.5
D 【解析】试题分析:∵Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,∴AB=2BC=4(cm),∵BC=2cm,D为BC的中点,动点E以1cm/s的速度从A点出发, ∴BD=BC=1(cm),BE=AB﹣AE=4﹣t(cm),若∠BED=90°,当A→B时,∵∠ABC=60°,∴∠BDE=30°,∴BE=BD=(cm),∴t=3.5,当B→A时,t=4+0.5=4...查看答案和解析>>
科目:初中数学 来源:2017年北师大版七年级数学下1.2幂的乘方与积的乘方同步练习(含答案) 题型:单选题
计算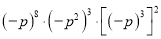 的结果是( )
的结果是( )
A. -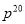 B.
B. 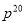 C. -
C. -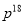 D.
D. 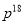
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 1.5 平方差公式 同步测试 题型:单选题
用简便方法计算40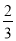 ×39
×39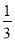 ,变形正确的是( )
,变形正确的是( )
A. (40+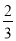 )(39+
)(39+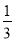 ) B. (40+
) B. (40+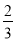 )(40-
)(40-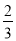 )
)
C. (40+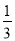 )(40-
)(40-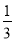 ) D. (40-
) D. (40-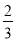 )(40-
)(40-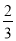 )
)
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:解答题
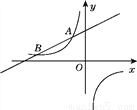
如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-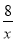 的图象交于A(-2,b),B两点.
的图象交于A(-2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:填空题
某市有长24000 m的新道路要铺上沥青,则铺路所需时间t(天)与铺路速度v(m/天)的函数关系式是______________.
t= (v>0) 【解析】试题解析:铺路所需要的时间t与铺路速度V之间的函数关系式是t=. 故答案为:t=.查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十六章 达标检测卷 题型:单选题
若在同一直角坐标系中,正比例函数y=k1x与反比例函数y= 的图象无交点,则有( )
的图象无交点,则有( )
A. k1+k2>0 B. k1+k2<0 C. k1k2>0 D. k1k2<0
D 【解析】当k1,k2同号时,正比例函数y=k1x与反比例函数y=的图象有交点;当k1,k2异号时,正比例函数y=k1x与反比例函数y=的图象无交点,即可得当k1k2<0时,正比例函数y=k1x与反比例函数y=的图象无交点,故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第1章 有理数 单元测试卷 题型:填空题
在数+8.3,-4,-0.8, 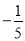 ,0,90,
,0,90, 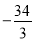 ,-|-24|中,负数有______________________________,分数有______________________________.
,-|-24|中,负数有______________________________,分数有______________________________.
查看答案和解析>>
科目:初中数学 来源:四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型:解答题
△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.
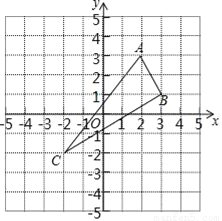
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
(1)作图见解析;(2)A2(2,﹣3),B2(3,﹣1),C2(﹣2,2);(3)6.5. 【解析】试题分析:(1)先得到△ABC关于y轴对称的对应点,再顺次连接即可; (2)先得到△ABC关于x轴对称的对应点,再顺次连接,并且写出△ABC关于x轴对称的△A2B2C2的各点坐标即可; (3)利用轴对称图形的性质可得利用矩形的面积减去三个顶点上三角形的面积即可. 试题解析:...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com