练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y=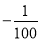x+150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w内（元）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳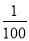x2元的附加费，设月利润为w外（元）．

    （1）当x=1000时，y= 元/件，w内= 元；

    （2）分别求出w内，w外与x间的函数关系式（不必写x的取值范围）；

    （3）当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值．

    （1）140；57500；（2）w内= x2+130x﹣62500，w外=x2+（150﹣a）x．（3）30. 【解析】 试题分析：（1）将x=1000代入函数关系式求得y，并根据等量关系“利润=销售额﹣成本﹣广告费”求得w内； （2）根据等量关系“利润=销售额﹣成本﹣广告费”“利润=销售额﹣成本﹣附加费”列出两个函数关系式； （3）对w内函数的函数关系式求得最大值，再求出...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：解答题

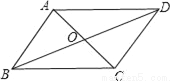
    （1）如图，在□ABCD中，对角线AC、BD相交于点O．请找出图中的一对全等三角形，并给予证明；

    （2）规定：一条弧所对的圆心角的度数作为这条弧的度数．

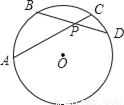
    ①如图，在⊙O中，弦AC、BD相交于点P，已知弧AB、弧CD分别为65°和45°，求∠APB；

    ②一般地，在⊙O中，弦AC、BD相交于点P，若弧AB、弧CD分别为m°和n°，求∠APB．

    （用m、n的代数式表示）

    （1）见解析；（2）①55°，②（m°+n°）． 【解析】【试题分析】 （1）答案不唯一，如：△AOB≌△COD．根据平行四边形的对角线相互平分，得AO=CO，OB=OD．因为对顶角相等，得∠AOB=∠COD，根据SAS，得：△AOB≌△COD． （2）①如图：连接AD， 根据弧AB、弧CD分别为65°和45°， 根据同弧所对的圆周角等于圆心角的一半，得∠ADB=65...

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：解答题

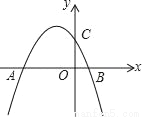
    已知抛物线y=﹣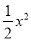+bx+c与y轴交于点C，与x轴的两个交点分别为A（﹣4，0），B（1，0）．

    （1）求抛物线的解析式；

    （2）已知点P在抛物线上，连接PC，PB，若△PBC是以BC为直角边的直角三角形，求点P的坐标；

    （3）已知点E在x轴上，点F在抛物线上，是否存在以A，C，E，F为顶点的四边形是平行四边形？若存在，请直接写出点E的坐标；若不存在，请说明理由．

    （1）抛物线的解析式为y=﹣；（2）存在，满足条件的P点坐标为（﹣4，0），P2（﹣5，﹣3）；（3）满足条件的点E为（﹣7，0）或（﹣1，0）或（，0）或（，0）． 【解析】试题分析：（1）因为抛物线经过点A（﹣4，0），B（1，0），所以可以设抛物线为y=﹣（x+4）（x﹣1），展开即可解决问题； （2）先证明∠ACB=90°，点A就是所求的点P，求出直线AC解析式，再求出过点B平...

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：单选题

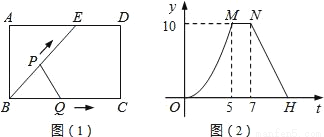
    如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是1cm/s，设P、Q出发t秒时，△BPQ的面积为y（cm2），已知y与t的函数关系的图象如图2（曲线OM为抛物线的一部分），则下列结论：

    ①AD=BE=5cm；②当0＜t≤5时，y=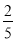t2；③直线NH的解析式为y=﹣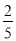t+27；④若△ABE与△QBP相似，则t=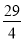秒，其中正确结论的个数为（　　）

    A. 4 B. 3 C. 2 D. 1

    B 【解析】试题分析：①根据图（2）可得，当点P到达点E时点Q到达点C， ∵点P、Q的运动的速度都是1cm/s， ∴BC=BE=5cm， ∴AD=BE=5（故①正确）； ②如图1，过点P作PF⊥BC于点F， 根据面积不变时△BPQ的面积为10，可得AB=4， ∵AD∥BC， ∴∠AEB=∠PBF， ∴sin∠PBF=sin∠AEB= ∴PF=PBsin∠PBF=t， ...

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：单选题

    若顺次连接四边形ABCD四边的中点，得到的图形是一个矩形，则四边形ABCD一定是（　　）

    A. 矩形 B. 菱形

    C. 对角线相等的四边形 D. 对角线互相垂直的四边形

    D 【解析】由于E、F、G、H分别是AB、BC、CD、AD的中点， 根据三角形中位线定理得：EH ∥ FG ∥ BD，EF ∥ AC ∥ HG； ∵四边形EFGH是矩形，即EF⊥FG， ∴AC⊥BD，即对角线互相垂直， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学二模试卷 题型：解答题

    先化简，再求值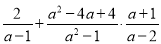： ，其中，a=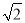+1．

    原式= ，当a=+1时，原式=. 【解析】试题分析：先因式分解，再根据分式的基本性质约分，然后算加，最后代入求值即可. 【解析】 原式 当时，原式.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学二模试卷 题型：填空题

    计算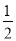：（﹣）﹣3+ +2sin45°+（）0=　 　．

    ﹣2． 【解析】根据实数的混合运算的法则，结合负整指数幂、二次根式、特殊角的三角函数值、零次幂的性质可得： （﹣）﹣3+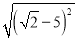 +2sin45°+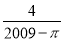（）0 =-8+5-++1 =-2 故答案为：-2.

    查看答案和解析>>

    科目：初中数学 来源：吉林省吉林市2016-2017年七年级上期期末数学试卷 题型：填空题

    如图，OC平分∠AOB，若∠AOC＝27°32′，则∠AOB＝________．

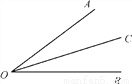
    55°4′ 【解析】∵OC平分∠AOB， ∴∠AOB=2∠AOC， 又∵∠AOC=27°32′， ∴∠AOB==27°32′×2=54°64′=55°4′.

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版七年级数学下册（广西）期末测试 题型：解答题

    如图1，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，得到A，B的对应点C，D，连接AC，BD，CD.

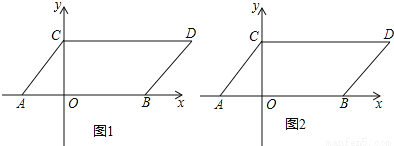
    (1)写出点C，D的坐标并求出四边形ABDC的面积；

    (2)在x轴上是否存在一点F，使得三角形DFC的面积是三角形DFB面积的2倍，若存在，请求出点F的坐标；若不存在，请说明理由；

    (3)如图2，点P是直线BD上的一个动点，连接PC，PO，当点P在直线BD上运动时，请直接写出∠OPC与∠PCD，∠POB的数量关系.

    (1)C(0，2)，D(4，2).8；（2）F(1，0)或(5，0)；（3）当点P在线段BD上运动时：∠OPC＝∠PCD＋∠POB；当点P在BD延长线上运动时：∠OPC＝∠POB－∠PCD；当点P在DB延长线上运动时：∠OPC＝∠PCD－∠POB. 【解析】试题分析：（1）根据点平移的规律易得点C的坐标为（0，2），点D的坐标为（4，2）；四边形ABDC的面积=2×（3+1）=8； （2）...

    查看答案和解析>>

    同步练习册答案