练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

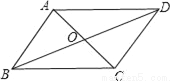
    （1）如图，在□ABCD中，对角线AC、BD相交于点O．请找出图中的一对全等三角形，并给予证明；

    （2）规定：一条弧所对的圆心角的度数作为这条弧的度数．

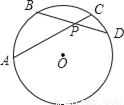
    ①如图，在⊙O中，弦AC、BD相交于点P，已知弧AB、弧CD分别为65°和45°，求∠APB；

    ②一般地，在⊙O中，弦AC、BD相交于点P，若弧AB、弧CD分别为m°和n°，求∠APB．

    （用m、n的代数式表示）

    （1）见解析；（2）①55°，②（m°+n°）． 【解析】【试题分析】 （1）答案不唯一，如：△AOB≌△COD．根据平行四边形的对角线相互平分，得AO=CO，OB=OD．因为对顶角相等，得∠AOB=∠COD，根据SAS，得：△AOB≌△COD． （2）①如图：连接AD， 根据弧AB、弧CD分别为65°和45°， 根据同弧所对的圆周角等于圆心角的一半，得∠ADB=65...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷（C卷） 题型：填空题

    有五张正面分别标有数字﹣2，﹣1，0，1，2的卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为a，则使关于x的一元二次方程x2﹣2（a﹣1）x+a（a﹣3）=0有两个不相等的实数根，且以x为自变量的二次函数y=x2﹣（a2+1）x﹣a+2的图象不经过点（1，0）的概率是__________．

    【解析】试题分析：∵使关于x的一元二次方程x2-2（a-1）x+a（a-3）=0有两个不相等的实数根， ∴[-2（a-1）]2-4×1×a（a-3）＞0， 解得：a＞-1， ∵以x为自变量的二次函数y=x2-（a2+1）x-a+2的图象不经过点（1，0）， ∴12-（a2+1）-a+2≠0， ∴a≠1且a≠-2， ∴满足条件的a只有0和2， ∴使关于x的一...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：解答题

    如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30º，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°，求大树的高度. （结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11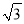， ≈1.73）

    13米． 【解析】试题分析：根据矩形性质得出DG=CH，CG=DH，再利用锐角三角函数的性质求出问题即可． 试题解析：如图，过点D作DG⊥BC于G，DH⊥CE于H， 则四边形DHCG为矩形． 故DG=CH，CG=DH， 在直角三角形AHD中， ∵∠DAH=30°，AD=6， ∴DH=3，AH=3， ∴CG=3， 设BC为x， 在直角三角形...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：单选题

    如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（　　）

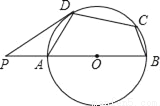
    A. 40° B. 35° C. 30° D. 45°

    C 【解析】试题分析：连接BD，∵∠DAB=180°﹣∠C=60°，∵AB是直径，∴∠ADB=90°，∴∠ABD=90°﹣∠DAB=30°，∵PD是切线，∴∠ADP=∠ABD=30°，故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：解答题

    如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.

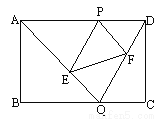
    （1）求证：△APE∽△ADQ；

    （2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？

    （3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）

    （1）证∠APE=∠ADQ，∠AEP=∠AQD. 注意到△APE∽△ADQ与△PDE∽△ADQ，及S△PEF=， 得S△PEF==. ∴当，即P是AD的中点时，S△PEF取得最大值. （3）作A关于直线BC的对称点A′，连DA′交BC于Q，则这个点Q就是使△ADQ周长最小的点，此时Q是BC的中点. 【解析】（1）证得∠APE=∠ADQ，∠AEP=∠AQD，即可得到△APE∽...

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：填空题

    一个口袋中有10个黑球和若干个白球若干个，从口袋中随机摸出一球，记下其颜色，再把它放回摇均，重复上述过程，共实验100次，其中25次摸到黑球，于是可以估计袋中共有白球_____个．

    30 【解析】∵共实验100次，其中25次摸到黑球， ∴黑球所占的比例为=0.25，设袋中共有白球x个，则=0.25， 解得：x=30个． 故本题答案为：30．

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：单选题

    如果圆锥的母线长为6cm，底面圆半径为3cm，则这个圆锥的侧面积为（　　）

    A. 9πcm2 B. 18πcm2 C. 27πcm2 D. 36πcm2

    B 【解析】底面圆半径为3cm，则底面周长=6π，圆锥的侧面积=×6π×6=18πcm2． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：填空题

    关于x一元二次方程2x（kx-4）-x2+6=0没有实数根，则k的最小整数值是 。

    2 【解析】试题分析：先把方程化为一般形式：（2k﹣1）x2﹣8x+6=0，由关于x的一元二次方程2x（kx﹣4）﹣x2+6=0没有实数根，所以2k﹣1≠0且△＜0，即解得k＞，即可得到k的最小整数值． 把方程化为一般形式：（2k﹣1）x2﹣8x+6=0， ∵原方程为一元二次方程且没有实数根， ∴2k﹣1≠0且△＜0，即△=（﹣8）2﹣4×（2k﹣1）×6=88﹣48k＜0...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学二模试卷 题型：解答题

    某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y=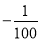x+150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w内（元）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳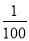x2元的附加费，设月利润为w外（元）．

    （1）当x=1000时，y= 元/件，w内= 元；

    （2）分别求出w内，w外与x间的函数关系式（不必写x的取值范围）；

    （3）当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值．

    （1）140；57500；（2）w内= x2+130x﹣62500，w外=x2+（150﹣a）x．（3）30. 【解析】 试题分析：（1）将x=1000代入函数关系式求得y，并根据等量关系“利润=销售额﹣成本﹣广告费”求得w内； （2）根据等量关系“利润=销售额﹣成本﹣广告费”“利润=销售额﹣成本﹣附加费”列出两个函数关系式； （3）对w内函数的函数关系式求得最大值，再求出...

    查看答案和解析>>

    同步练习册答案