
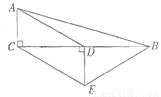
如图,在△ABC, 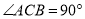 中,D是BC的中点,DE⊥BC,CE∥AD,若
中,D是BC的中点,DE⊥BC,CE∥AD,若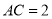 ,
, 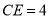 ,求四边形ACEB的周长.
,求四边形ACEB的周长.
科目:初中数学 来源:2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型:单选题
不等式组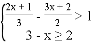 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A. 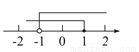
B. 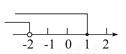
C. 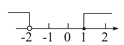
D. 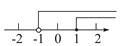
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《实际问题与二元一次方程组》同步练习 题型:单选题
食堂的存煤计划用若干天,若每天用130kg,则缺少60kg;若每天用120kg,则还剩余60kg.设食堂的存煤共有xkg,计划用y天,则下面所列方程组正确的是( )
A. 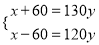 B.
B. 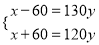
C. 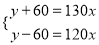 D.
D. 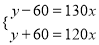
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《消元解二元一次方程组》同步练习 题型:单选题
若方程mx+ny=6有两个解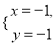
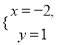 ,则m,n的值为( )
,则m,n的值为( )
A. 4,2 B. 2,4 C. -4,-2 D. -2,-4
C 【解析】试题分析:把, 代入mx+ny=6中, 得: , 解得: . 故选C.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:解答题
如图,在□ABCD中,AD=4cm,∠A=60°,BD⊥AD.一动点P从A出发,以每秒1cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD.
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿A→B的路线运动,且在AB上以每秒1cm的速度匀速运动,(当P、Q中的某一点到达终点,则两点都停止运动.)过Q作直线QN,使QN∥PM,设点Q运动的时间为t秒(0≤t≤8),直线PM与QN截□ABCD所得图形的面积为S(cm2).求S关于t的函数关系式.
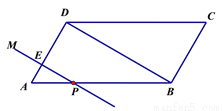
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:填空题
在Rt△ABC中,AC=5,BC=12,则AB边的长是______________.
13或 【解析】试题分析:当AB为斜边时,则AB=;当AB为直角边时,则AB=,则AB边的长为13或.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:单选题
小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,则旗杆的高是( ).
A. 8米 B. 10米 C. 12米 D. 14米
C 【解析】 画出示意图如下所示: 设旗杆的高AB为xm,则绳子AC的长为(x+1)m, 在Rt△ABC中,AB2+BC2=AC2, ∴x2+52=(x+1)2, 解得:x=12, ∴AB=12m, 即旗杆的高是12m. 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版八年级上册数学全册综合测试卷 题型:填空题
在3和4之间找出两个无理数:________和________.
π 【解析】∵3<π<4,3<<4, ∴在3和4之间找出两个无理数:π和.(答案不唯一)查看答案和解析>>
科目:初中数学 来源:湖南省长沙市2017-2018学年九年级(上)第一次月考数学试卷 题型:解答题
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com