
��ʦ������һ����600������ˮ�ܵ����ƻ�������Сʱ��ɣ���ʵ�ʼ������У�ÿСʱ���ܵ�������ԭ�ƻ���1.2���������ǰ2Сʱ���������ʦ��ԭ�ƻ�ÿСʱ���ܵ������ף�
50�� �������� �����������ԭ�ƻ�ÿСʱ���ܵ�Ϊxm����ʵ��ʩ��ÿ������ܵ�Ϊ1.2xm��������ϵΪ��ԭ�ƻ���ɵ�������ʵ����ɵ�����=2�����������ϵ�г�������⼴�ɣ� �����������ԭ�ƻ�ÿСʱ���ܵ�x�ף� �����⣬�ã� ���x=50�� �����飬x=50��ԭ���̵Ľ⣮�ҷ������⣮ ��ԭ�ƻ�ÿСʱ���ܵ�50�ף�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������������2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
һ�κ���y=kx+b(k,bʵ��������k��0)��ͼ����ͼ��ʾ��
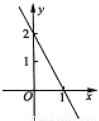
��1����k��b��ֵ��
��2����-1<x<1ʱ����y��ȡֵ��Χ.
��1������2��0�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹŶ�����˹��2017-2018ѧ���һѧ�������Ծ���һ��ѧ. ���ͣ���ѡ��
������(-2)2��- ح-3|��-(-2)3��-(+(-3))�и����ĸ����ǣ� ��
A. 1 B. 2 C. 3 D. 4
A ��������(-2)2=4, - ح-3|=-3, -(-2)3=8, -(+(-3))=3,�⼸����������,������- ح-3|��1��, ��ѡ:A.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����ϳ���������ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ� ���ͣ���ѡ��
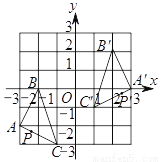
��ͼ����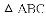
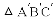 �����
�����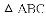
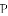
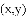
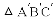 �еĶ�Ӧ��
�еĶ�Ӧ��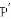 ������Ϊ�� ����
�������� ����
A. 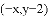
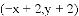
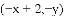
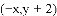
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧģ���Ծ� ���ͣ������
��ͼ���ھ���ABCD�У�AB=6cm��AD=8cm����P�ӵ�B�������ضԽ���BD���D�����˶����ٶ�Ϊ4cm/s������P��PQ��BD��BC�ڵ�Q����PQΪһ����������PQMN��ʹ�õ�N��������PD�ϣ���O�ӵ�D��������DC���C�����˶����ٶ�Ϊ3cm/s����OΪԲ�ģ�0.8cmΪ�뾶��ԲO����P���Oͬʱ�����������ǵ��˶�ʱ��Ϊt����λ��s����0��t��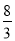 ��
��
��1����ͼ1������DQ����DQƽ�֡�BDCʱ��t��ֵΪ�� ��
��2����ͼ2������CM������CMQ����CQΪ�ĵ��������Σ���t��ֵ��
��3�������������̽����������������⣺
��֤�������˶������У���Oʼ����QM����ֱ�ߵ���ࣻ
����ͼ3�����˶������У���QM��ԲO����ʱ����t��ֵ�����жϴ�ʱPM��ԲO�Ƿ�Ҳ���У�˵�����ɣ�
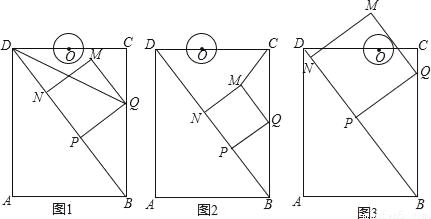
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧģ���Ծ� ���ͣ������
��ͼ��������ABCD�ı߳�Ϊ2����E��F�ֱ��ڱ�AD��CD�ϣ�����EBF=45�㣬���EDF���ܳ�����_____��
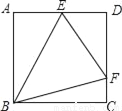
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧģ���Ծ� ���ͣ���ѡ��
��ͼ��Rt��ABC�У���C=90�㣬��ABC=30�㣬AC=2����ABC�Ƶ�C˳ʱ����ת�á�A1B1C����A1����AB����ʱ������B1B��ȡBB1���е�D������A1D����A1D�ij����� ��������
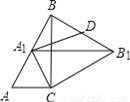
A. 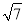 B.
B. 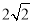 C. 3 D.
C. 3 D. 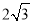
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡͭ����������2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
�ڡ�ABC�У���A=30�㣬��B=45�㣬AC=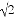 ����BC=__________��
����BC=__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ��� ���꼶��ѧ��ĩ���Ծ� ���ͣ������
��ͼ���۵�������ֽƬABCD�����۳��ۺۣ��Խ��ߣ�BD�����۵���ʹAD���ڶԽ���BD�ϣ����ۺ�DG����AB=4��BC=3����DG�ij�.
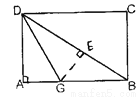
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com