
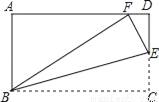
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为_____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:吉林省长春市宽城区2017年中考数学一模试卷 题型:填空题
分解因式:a3﹣2a2+a=________.
a(a﹣1)2 【解析】试题分析:此多项式有公因式,应先提取公因式a,再对余下的多项式进行观察,有3项,可利用完全平方公式继续分解.a3﹣2a2+a=a(a2﹣2a+1)=a(a﹣1)2.故答案为:a(a﹣1)2.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年七年级上册期末模拟数学试卷 题型:解答题
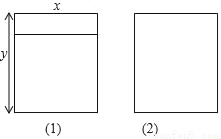
如图所示,是两种长方形铝合金窗框,已知窗框的长都是y米,窗框宽都是x米,若一用户需(1)型的窗框2个,(2)型的窗框5个.则共需铝合金多少米?(用含x、y的式子表示)
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年七年级上册期末模拟数学试卷 题型:单选题
一副直角三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )
A. 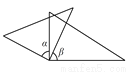 B.
B. 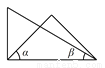 C.
C. 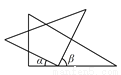 D.
D. 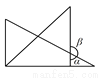
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学模拟试卷 题型:解答题
如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
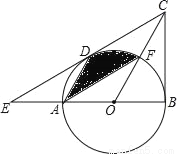
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学模拟试卷 题型:单选题
一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则用来表示y与x之间关系的选项是( )
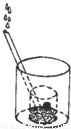
A. 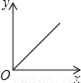 B.
B. 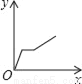 C.
C. 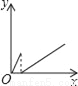 D.
D. 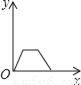
查看答案和解析>>
科目:初中数学 来源:甘肃省张掖市2017-2018学年七年级(上)期中数学试卷 题型:填空题
如果向东走6米记作+6米,那么向西走10米记作_____.
-10米 【解析】试题分析:相反意义的量包含两层意思:一是它们意义相反符号相反;二是它们都表示一定的数量(在数量上它们不一定相同).则向西走10米记作-10米.查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级12月月考数学试卷 题型:解答题
已知一次函数y=kx-6,当x=1时,y=2。求:
(1)k的值;
(2)当0≤x≤3时,求y的取值范围。
(1)k=8;(2)-6《y《18. 【解析】试题分析:(1)把x=1,y=2代入y=kx-6,即可求得k的值; (2)先根据一次函数的性质判断出函数的增减性,再求出y最大值和最小值即可解答. 试题解析:(1)x=1,y=2代入y=kx-6中, 得: 2=k-6, 解得k=8; (2)∵一次函数y=8x-6中k=8>0, ∴一次函数y=8x-6是增函数, ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com