练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果矩形的宽与长的比是黄金比，我们称这样的矩形为黄金矩形，如图，明明这样画了一个矩形DCEF，

    (1)作边长为2的正方形ABCD

    (2)取BC的中点M，连接DM

    (3)延长BC至E，使ME＝MD

    (4)过E点作EF⊥BE交AD的延长线于F点

    试说明矩形DCEF为黄金矩形．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    知识背景：恩施来凤有一处野生古杨梅群落，其野生杨梅是一种具特殊价值的绿色食品．在当地市场出售时，基地要求“杨梅”用双层上盖的长方体纸箱封装（上盖纸板面积刚好等于底面面积的2倍，如图）
    （1）实际运用：如果要求纸箱的高为0.5米，底面是黄金矩形（宽与长的比是黄金比，取黄金比为0.6），体积为0.3立方米．
    ①按方案1（如图）做一个纸箱，需要矩形硬纸板A1B1C1D1的面积是多少平方米？
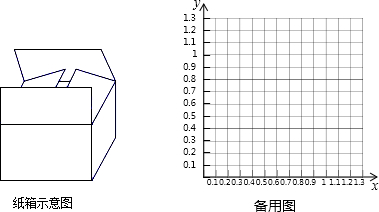
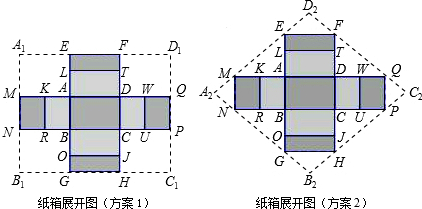
    精英家教网
    ②小明认为，如果从节省材料的角度考虑，采用方案2（如图）的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优，你认为呢？请说明理由．
    精英家教网
    （2）拓展思维：北方一家水果商打算在基地购进一批“野生杨梅”，但他感觉（1）中的纸箱体积太大，搬运吃力，要求将纸箱的底面周长、底面面积和高都设计为原来的一半，你认为水果商的要求能办到吗？请利用函数图象验证．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    知识背景：恩施来凤有一处野生古杨梅群落，其野生杨梅是一种具特殊价值的绿色食品．在当地市场出售时，基地要求“杨梅”用双层上盖的长方体纸箱封装（上盖纸板面积刚好等于底面面积的2倍，如图）
    实际运用：如果要求纸箱的高为0.5米，底面是黄金矩形（宽与长的比是黄金比，取黄金比为0.6），体积为0.3立方米．
    ①按方案1（如图）做一个纸箱，需要矩形硬纸板A1B1C1D1的面积是多少平方米？
    ②小明认为，如果从节省材料的角度考虑，采用方案2（如图）的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优，你认为呢？请说明理由．

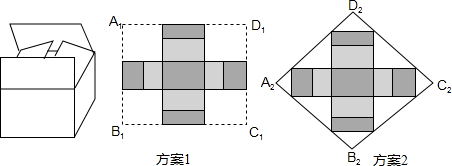
    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年湖北省宜昌中学八年级下学期期中考试数学试卷（带解析） 题型：解答题

    如果一个矩形的宽与长的比是，那么这个矩形就是一个黄金矩形。在黄金矩形ABCD的内部作一个正方形CDFE后，得到一个新的矩形ABFE,那么ABFE也是黄金矩形吗？

    查看答案和解析>>

    科目：初中数学 来源：2014届湖北省八年级下学期期中考试数学试卷（解析版） 题型：解答题

    如果一个矩形的宽与长的比是，那么这个矩形就是一个黄金矩形。在黄金矩形ABCD的内部作一个正方形CDFE后，得到一个新的矩形ABFE,那么ABFE也是黄金矩形吗？

     

    查看答案和解析>>

    同步练习册答案