
已知:如图,二次函数y=a(x﹣h)2+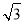 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
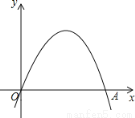
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
(1)直线x=1 (2)点A′为抛物线y=﹣(x﹣1)2+的顶点 【解析】 试题分析:(1)把已知点O、A代入函数的解析式可求出h的值h=1,及a=,然后根据二次函数的顶点式的特点判断出对称轴; (2)由线段OA绕点O逆时针旋转60°到OA′,可知OA′=OA=2,∠A′OA=60°,如图,作A′B⊥x轴于点B,根据直角三角形的特点可知sin60°=,cos60°=,因此可求得A... 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.1 二次函数 题型:单选题
圆的面积公式S=πR2中,S与R之间的关系是( )
A. S是R的正比例函数 B. S是R的一次函数
C. S是R的二次函数 D. 以上答案都不对
C 【解析】根据二次函数的定义,易得S是R的二次函数,故选C.查看答案和解析>>
科目:初中数学 来源:人教七年级下册数学第九章-不等式与不等式组单元测试 题型:填空题
若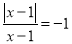 ,则x的取值范围是____________.
,则x的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
对于二次函数y=-x2+2x,有下列四个结论:①它的对称轴是直线x=1;②设y1=-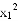 +2x1,y2=-
+2x1,y2=-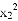 +2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确结论的个数为( )
+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
C 【解析】试题分析:利用配方法求出二次函数对称轴,再求出图象与x轴交点坐标,进而结合二次函数性质得出答案. y=﹣x2+2x=﹣(x﹣1)2+1,故①它的对称轴是直线x=1,正确; ②∵直线x=1两旁部分增减性不一样, ∴设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1或y2<y1,错误; ③当y=0,则x(﹣x+2)=0,解得:x1=0,x2=2, ...查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A. x1=0,x2=6 B. x1=1,x2=7 C. x1=1,x2=﹣7 D. x1=﹣1,x2=7
D 【解析】试题分析:先根据二次函数y=x2+mx的对称轴是x=3求出m的值,再把m的值代入方程x2+mx=7,求出x的值即可. ∵二次函数y=x2+mx的对称轴是x=3, ∴﹣=3,解得m=﹣6, ∴关于x的方程x2+mx=7可化为x2﹣6x﹣7=0,即(x+1)(x﹣7)=0,解得x1=﹣1,x2=7.查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
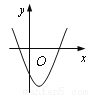
已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
A. 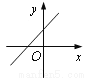 B.
B. 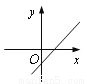 C.
C. 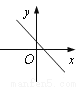 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:填空题
已知函数y=-(x-1)2图象上两点A(2,y1),B(a,y2),其中a>2,则y1与y2的大小关系是y1_____y2.(填“<”“>”或“=”)
> 【解析】试题分析:根据函数表达式可以判断抛物线对称轴是x=1,开口向下,所以当x>1时,y随x的增大而减小,a>2,所以y1>y2查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
在平面直角坐标系中,将抛物线y=x2-4向上平移2个单位长度,得到的抛物线表达式为( )
A. y=(x+2)2 B. y=x2+2
C. y=(x-2)2 D. y=x2-2
D 【解析】试题分析:抛物线的对称轴是y轴,顶点在y轴上,(0,-4)向上平移两个单位则顶点坐标变为(0,-2),所以抛物线表达式是y=x2-2,故选D.查看答案和解析>>
科目:初中数学 来源:上海市浦东新区第四教育署2017-2018学年八年级(五四学制)上学期期中质量调研数学试卷 题型:单选题
下列命题中是假命题的是( )
A. 直角的补角是直角
B. 两直线平行,一组同旁内角的角平分线互相垂直
C. 等腰三角形的高、中线、角平分线三线合一
D. 有两角及其中一角的平分线对应相等的两个三角形全等
C 【解析】试题解析:A. 直角的补角是直角,该说法正确,故是真命题; B. 两直线平行,一组同旁内角的角平分线互相垂直,该说法正确,故是真命题; C. 等腰三角形的底边上的高、底边上的中线、顶角角平分线三线合一,原说法错误,故是假命题; D. 有两角及其中一角的平分线对应相等的两个三角形全等,该说法正确,故是真命题. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com