练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知x1，x2 是关于x的方程（x－2）（x－m）=（p－2）（p－m）的两个实数根．

    （1）求x1，x2 的值；

    （2）若x1，x2 是某直角三角形的两直角边的长，问当实数m，p满足什么条件时，此直角三角形的面积最大？并求出其最大值．

    （1）x1 = p，x2 = m + 2－p； （2）当且m＞－2时，以x1，x2为两直角边长的直角三角形的面积最大，最大面积为（或）． 【解析】试题分析：（1）化简方程，用分解因式法求出两根； （2）直角三角形的面积为x1x2，利用根与系数的关系可以得到关于p的关系式，然后利用二次函数可以求出什么时候有最大值． 试题解析：（1） 原方程变为：x2－（m + 2）x + 2...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    同一条直线上有若干个点，若构成的射线共有10条，则构成的线段共有_____条.

    10 【解析】【解析】 ∵同一直线上有若干个点，构成的射线共有10条，∴这条直线上共有5个点，∴构成的线段条数： =10，故答案为：10．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型：解答题

    如图1，抛物线y=-x2+bx+c与x轴相交于点A，C，与y轴相交于点B，连接AB，BC，点A的坐标为（2，0），tan∠BAO=2，以线段BC为直径作⊙M交AB于点D，过点B作直线l∥AC，与抛物线和⊙M的另一个交点分别是E，F．

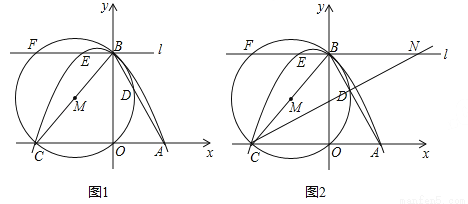
    （1）求该抛物线的函数表达式；

    （2）求点C的坐标和线段EF的长；

    （3）如图2，连接CD并延长，交直线l于点N，点P，Q为射线NB上的两个动点（点P在点Q的右侧，且不与N重合），线段PQ与EF的长度相等，连接DP，CQ，四边形CDPQ的周长是否有最小值？若有，请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值；若没有，请说明理由．

    （1）抛物线的解析式为y=-x2-x+4．（2）2．（3）2+2+2． 【解析】 试题分析：（1）根据点A的坐标和tan∠BAO=2求得AO=2，BO=4，从而求得点B的坐标为（0，4），利用待定系数法求得二次函数的解析式即可． （2）首先根据抛物线的对称轴求得点A的对称点C的坐标，然后求得点B的对称点E的坐标为（-1，4），从而求得BE的长，得到EF的长即可； （3）作点...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型：填空题

    正六边形的每个中心角为_________度．

    60 【解析】正六边形的圆心角等于一个周角，即为360° ，正六边形有6个中心角， 所以每个中心角=360°÷6=60°， 故答案为：60.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型：单选题

    若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（　　）

    A. k＞﹣1 B. k＞﹣1且k≠0 C. k＜1 D. k＜1且k≠0

    B 【解析】试题解析：∵关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根， ∴k≠0且△＞0，即（-2）2-4×k×（-1）＞0， 解得k＞-1且k≠0． ∴k的取值范围为k＞-1且k≠0． 故选B.

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市蓬溪县2018届九年级上学期期末考试数学试卷 题型：解答题

    将分别标有数字2,3,5的三张颜色、质地、大小完全一样的卡片背面朝上放在桌面上.

    （1）随机抽取一张,求抽到奇数的概率；

    （2）随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并画树状图或列表求出抽取到的两位数恰好是35的概率.

    （1）P（抽到奇数）=；（2）P（恰好抽到为35）= 【解析】试题分析：（1）先求出这组数中奇数的个数，再利用概率公式解答即可； （2）根据题意列举出能组成的数的个数及35的个数，再利用概率公式解答． 试题解析：（1）根据题意可得：有三张卡片，奇数只有“3和5”一张，故抽到奇数的概率P=； （2）根据题意可得：随机抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数...

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市蓬溪县2018届九年级上学期期末考试数学试卷 题型：填空题

    两个相似三角形周长的差是4cm，面积的比是16:25，那么这两个三角形的周长分别是__________cm和____________cm

    16 20 【解析】试题解析：∵两个相似三角形面积的比是16:25， ∴两个相似三角形周长比为4:5. 由题意，可设较小三角形的周长为4xcm，则较大三角形的周长为5xcm， 则有：5x-x=4，解得x=4， ∴这两个三角形的周长分别是16cm和20cm. 故答案为：16，20.

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型：解答题

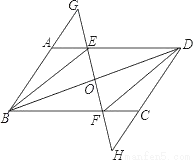
    已知：如图，在?ABCD中，E，F分别是边AD，BC上的点，且AE=CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点O．

    （1）求证：△ABE≌△CDF；

    （2）连接DG，若DG=BG，则四边形BEDF是什么特殊四边形？请说明理由．

    （1）证明见解析；（2）四边形BEDF是菱形，理由见解析. 【解析】试题分析：（1）由平行四边形的性质得出AB=CD，∠BAE=∠DCF，由SAS证明△ABE≌△CDF即可；（2）由平行四边形的性质得出AD∥BC，AD=BC，证出DE=BF，得出四边形BEDF是平行四边形，得出OB=OD，再由等腰三角形的三线合一性质得出EF⊥BD，即可得出四边形BEDF是菱形． 试题解析：（1）证明：...

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    下列说法：?-a是负数；?-2的倒数是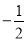；?-（-3）的相反数是-3；④绝对值等于2的数2.其中正确的是（ ）

    A. 1个 B. 2 个 C. 3个 D. 4个

    B 【解析】因为a是不确定的数,所以?－a是负数错误,根据倒数的定义可得:－2的倒数是,所以?正确,根据相反数的定义, －（－3）的相反数是－3,所以?正确, 根据绝对值的定义,绝对值等于2的数是2和－2,所以④错误,故选B.

    查看答案和解析>>

    同步练习册答案