
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源:甘肃省张掖市高台县2016-2017学年八年级(上)期末数学试卷 题型:单选题
对于两组数据A,B,如果sA2>sB2,且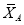 =
=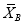 ,则( )
,则( )
A. 这两组数据的波动相同 B. 数据B的波动小一些
C. 它们的平均水平不相同 D. 数据A的波动小一些
B 【解析】试题解析:方差越小,波动越小. 数据B的波动小一些. 故选B.查看答案和解析>>
科目:初中数学 来源:重庆市江北区2018届九年级上期末模拟数学试卷 题型:填空题
如图所示,以边长为2的等边△ABO的顶点O为坐标原点,点B在x轴上,则经过点A的反比例函数的表达式为________
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:解答题
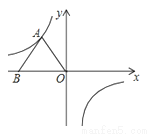
如图1,正方形ABCD的一边AB在直尺一边所在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E.
(1)如图1,线段AB与OE之间的数量关系为 .(请直接填结论)
(2)保证点A始终在直线MN上,正方形ABCD绕点A旋转θ(0<θ<90°),过点 B作BF⊥MN于点F.
①如图2,当点O、B两点均在直线MN右侧时,试猜想线段AF、BF与OE之间存在怎样的数量关系?请说明理由.
②如图3,当点O、B两点分别在直线MN两侧时,此时①中结论是否依然成立呢?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
③当正方形ABCD绕点A旋转到如图4的位置时,线段AF、BF与OE之间的数量关系为 .(请直接填结论)
(1)AB=2OE;(2)①AF+BF=2OE,证明见解析;②AF﹣BF=2OE 证明见解析;③BF﹣AF=2OE, 【解析】试题分析:(1)利用直角三角形斜边的中线等于斜边的一半即可得出结论; (2)①过点B作BH⊥OE于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:填空题
在平面坐标系中,正方形ABCD的位置如图,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交于x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2016个正方形A2015B2015C2015C2014的面积为_____.
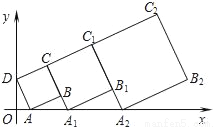
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. 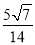 B.
B. 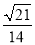 C.
C. 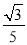 D.
D. 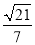
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
﹣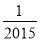 的倒数是( )
的倒数是( )
A. 2015 B. ﹣2015 C. 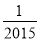 D. ﹣
D. ﹣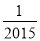
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:填空题
分解因式2x2﹣4x+2的最终结果是_____.
2(x﹣1)2 【解析】试题分析:先提取公因式2,再根据完全平方公式进行二次分解. 试题解析:2x2-4x+2, =2(x2-2x+1), =2(x-1)2.查看答案和解析>>
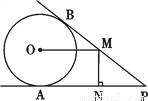
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:解答题
如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM = AN;
(2)若⊙O的半径R = 3,PA = 9,求OM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com