
钟表上2时30分时,时针与分针所成的锐角的度数是_____.
105° 【解析】因为2时30分时,时针指向2与3的中间,分针指向6.钟表12个数字,每相邻两个数字之间的夹角为30°,所以2时30分时分针与时针的夹角是3×30°+15°=105°.科目:初中数学 来源:广东省初中部2017-2018学年第一学期期末模拟测试七年级数学试卷 题型:单选题
A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行。已知甲车速度为120千米/小时,乙车速度为80千米/小时,经过t小时两车相距50千米,则t的值是( )
A. 2 B. 2或2.25 C. 2.5 D. 2或2.5
D 【解析】试题分析:如果甲、乙两车是在环形车道上行驶,则本题应分两种情况进行讨论: 一、两车在相遇以前相距50千米,在这个过程中存在的相等关系是:甲的路程+乙的路程=(450﹣50)千米; 二、两车相遇以后又相距50千米.在这个过程中存在的相等关系是:甲的路程+乙的路程=450+50=500千米. 已知车的速度,以及时间就可以列代数式表示出路程,得到方程,从而求出时间t的...查看答案和解析>>
科目:初中数学 来源:云南省2016-2017学年七年级上学期期末考试数学试卷 题型:解答题
计算: 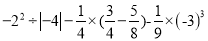
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型:解答题
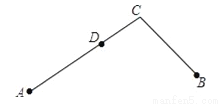
如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如果点D是折线A﹣C﹣B的“折中点”,请解答以下问题:
(1)已知AC=m,BC=n.
当m>n时,点D在线段 上;
当m=n时,点D与 重合;
当m<n时,点D在线段 上;
(2)若E为线段AC中点,EC=4,CD=3,求CB的长度.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型:解答题
解下列一元一次方程:
(1)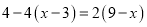 (2)
(2)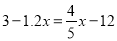
(3)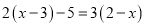 (4)
(4)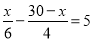
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型:填空题
若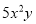 和
和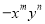 是同类项,则
是同类项,则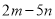 =______.
=______.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型:单选题
已知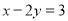 ,那么代数式
,那么代数式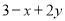 的值是( )
的值是( )
A. ﹣3 B. 0 C. 6 D. 9
B 【解析】已知,代数式=3-(x-2y)=3-3=0,故选B.查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年八年级上学期期末测评数学试卷 题型:填空题
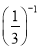
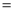 ______;
______; 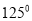
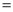 _______
_______
查看答案和解析>>
科目:初中数学 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
(8分)已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.
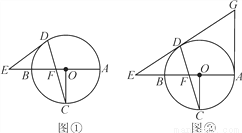
(1)如图①,求证:ED为⊙O的切线;
(2)如图②,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.
(1)见解析;(2)12 【解析】试题分析:(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线; (2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com