练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列命题中错误的命题是（　　）

    A. （﹣3）2的平方根是±3

    B. 平行四边形是中心对称图形

    C. 单项式5x2y与﹣5xy2是同类项

    D. 近似数3.14×103有三个有效数字

    C 【解析】试题分析：同类项是含有相同的字母，且字母的指数也相同的单项式.故C错，选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型：填空题

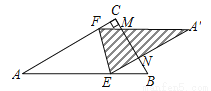
    如图，已知△ABC中，∠C=90°，∠A=30°，AB=11，点E、F分别在AB、AC上，沿EF折叠△ABC，点A的对应点为点A′，A′E、A′F交BC于点M、N．若AE=8，当△A′MN与△ABC相似时，则AF =________．

    或8． 【解析】分类讨论：（1）若 ，则M与C重合，即A、C、A’共线，则，因为∠A=30°， 即 ，解得 . （2）若 ，则 ，因为 ， ，根据对折，则 ,则AF=AE=8. 综上述，AF =或8.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：单选题

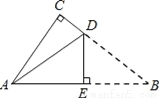
    如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）

    A. 4cm B. 5cm C. 6cm D. 10cm

    B 【解析】试题分析：先根据勾股定理求出AB的长，再由图形折叠的性质可知，AE=BE，故可得出结论． ∵△ABC是直角三角形，两直角边AC=6cm、BC=8cm， ∴AB===10cm， ∵△ADE由△BDE折叠而成， ∴AE=BE=AB=×10=5cm．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017届九年级上学期第二次月考数学试卷 题型：解答题

    已知抛物线过（1，0）、（3，0）、（﹣1，1）三点，求它的函数关系式．

    二次函数的解析为y=﹣x2+ x+ ． 【解析】试题分析：设解析式为y=ax2+bx+c，将三点代入解析式求a、b、c的值即可得到二次函数的解析式. 设二次函数的解析为y=ax2+bx+c， ∵图象经过点（1，0）、（3，0）、（﹣1，1）， ∴代入可得 ，∴ ， ∴二次函数的解析为y=﹣x2+ x+ ．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017届九年级上学期第二次月考数学试卷 题型：单选题

    将抛物线y=2x2﹣12x+16绕它的顶点旋转180°，所得抛物线的解析式是（　　）

    A. y=﹣2x2﹣12x+16 B. y=﹣2x2+12x﹣16

    C. y=﹣2x2+12x﹣20 D. y=﹣2x2+12x﹣19

    C 【解析】试题分析：绕顶点旋转180°，抛物线开口大小，形状均不变，顶点坐标也不变，开口方向相反，将原抛物线变成顶点式是y=2(x-3)2-2,旋转之后顶点坐标不变，开口相反则抛物线变成y=-2(x-3)2-2，所以变成一般形式是y=﹣2x2+12x﹣20.故选C.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第24章小结与复习 练习 题型：解答题

    如图,⊙O 的半径为１,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM＝PN．

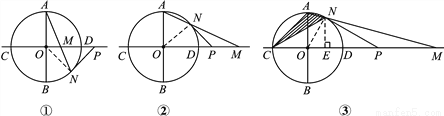
    (1)当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;

    (2)当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立? 请说明理由;

    (3)当点 M 在⊙O 外部,如图③,∠AMO＝15°,求图中阴影部分的面积．

    (1)详见解析；（2）成立，理由详见解析；（3）＋－． 【解析】试题分析：（1）PN 与⊙O 相切．要证明ONPN即可，连接ON，PM＝PN，所以∠PNM＝∠PMN，∠AMO＝∠PMN，AB⊥CD,所以∠PMN+∠MAO=90°，又因∠MAO=∠MNO,所以∠PNM+∠MNO=90°，所以PN 与⊙O 相切．（2）成立，进行等量代换，∠MAO+∠OMA=90°，因∠OMA=∠PNM，∠MAO...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第24章小结与复习 练习 题型：填空题

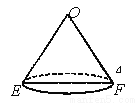
    如图是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF长为10 cm，母线OE（OF）长为10 cm．在母线OF上的点A处有一块爆米花残渣，且FA = 2 cm，一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点，则此蚂蚁爬行的最短距离为_________.

    cm 【解析】试题分析：因为OE=OF=EF=10（cm）， 所以底面周长=10π（cm）， 将圆锥侧面沿OF剪开展平得一扇形，此扇形的半径OE=10（cm），弧长等于圆锥底面圆的周长10π（cm） 设扇形圆心角度数为n，则根据弧长公式得： 10π=， 所以n=180°， 即展开图是一个半圆， 因为E点是展开图弧的中点， 所以∠EOF=90°，...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第24章小结与复习 练习 题型：单选题

    已知⊙O的直径为3cm ， 点P到圆心O的距离OP=2cm ， 则点P（  ）

    A. 在⊙O外                             B. 在⊙O上                             C. 在⊙O内                             D. 不能确定

    A 【解析】试题分析：⊙O 的直径为3cm,则圆的半径是1.5cm, OP＝2cm,所以OP>r，所以点P在⊙O 外.故选A.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（1）练习 题型：填空题

    已知圆的半径等于10厘米，直线和圆只有一个公共点，则圆心到直线的距离是________．

    10厘米. 【解析】∵直线和圆则有一个公共点，∴直线与圆相切，∴d=r， ∵圆的半径等于10厘米， ∴圆心到直线l的距离是10厘米， 故答案为：10厘米．

    查看答案和解析>>

    同步练习册答案