
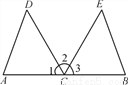
如图所示,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
(1)试说明:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
科目:初中数学 来源:重庆市江津区2016-2017学年七年级下学期期末考试数学试卷 题型:填空题
王强参加3 000米长跑,他以6米/秒的速度跑了一段路程后,又以4米/秒的速度跑完了其余的路程,一共花了10分钟,求他以6米/秒的速度跑了多少米?设他以6米/秒的速度跑了x米,则列出的方程是___________.
【解析】设他以6米/秒的速度跑了x米,则他以4米/秒的速度跑了(3000-x)米,根据跑完全程共用10分钟可得方程.查看答案和解析>>
科目:初中数学 来源:2016-2017学年山西农业大学附中七年级(下)第二次月考数学试卷 题型:单选题
(﹣2xy)4的计算结果是( )
A. ﹣2x4y4 B. 8x4y4 C. 16x4y4 D. 16xy4
C 【解析】试题解析:(-2xy)4=(-2)4x4y4=16x4y4. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年海南省文昌市中考数学模拟试卷 题型:单选题
在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( )
A. (3,﹣3) B. (﹣3,3) C. (3,3)或(﹣3,﹣3) D. (3,﹣3)或(﹣3,3)
D 【解析】试题解析:∵把点P(-5,3)向右平移8个单位得到点P1, ∴点P1的坐标为:(3,3), 如图所示:将点P1绕原点逆时针旋转90°得到点P2,则其坐标为:(-3,3), 将点P1绕原点顺时针旋转90°得到点P3,则其坐标为:(3,-3), 故符合题意的点的坐标为:(3,-3)或(-3,3). 故选D.查看答案和解析>>
科目:初中数学 来源:2017年海南省文昌市中考数学模拟试卷 题型:单选题
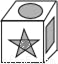
将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A. 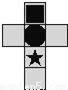 B.
B. 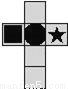 C.
C. 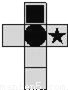 D.
D. 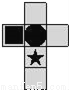
查看答案和解析>>
科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:解答题
)先化简,再求值:(a+2)2-(a+1)(a-1),其中a=-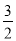 .
.
查看答案和解析>>
科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:单选题
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
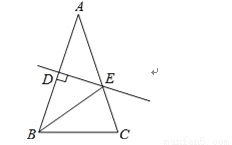
A.13B.14C.15D.16
A 【解析】 试题分析:∵DE是AB的垂直平分线, ∴AE=BE, ∴△BEC周长=BE+CE+BC=AE+CE+BC=AC+BC, ∵腰长AB=8, ∴AC=AB=8, ∴△BEC周长=8+5=13. 故选A.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知:如图,四边形ABCD中,AB⊥BC,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
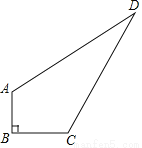
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:解答题
如图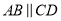 ,
, 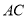 平分
平分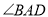 ,
, 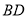 平分
平分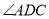 ,
, 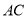 和
和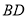 交于点
交于点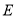 ,
, 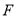 为
为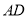 的中点,连结
的中点,连结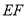 .
.
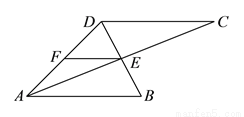
(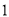 )找出图中所有的等腰三角形.
)找出图中所有的等腰三角形.
(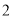 )若
)若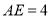 ,
, 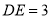 ,求
,求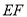 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com