练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知一组数据1，3，5，7，则该组数据的方差S2=_________.

    5 【解析】, ∴.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    点（－3，4）关于y轴的对称点的坐标是 （ ）

    A. （-3，-4） B. （3，4） C. （3，-4） D. （4，-3）

    B 【解析】试题解析：点P（-3，4）关于y轴对称点的坐标为（3，4）． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    在数轴上与﹣2所对应的点相距4个单位长度的点表示的数是_____．

    2或﹣6 【解析】【解析】 当该点在﹣2的右边时，由题意可知：该点所表示的数为2，当该点在﹣2的左边时，由题意可知：该点所表示的数为﹣6．故答案为：2或﹣6．

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，⊙O是△ABC的外接圆，∠ABC=45°，OC∥AD，AD交BC的延长线于D，AB交OC于E．

    （1）求证：AD是⊙O的切线；

    （2）若⊙O的直径为6，线段BC=2，求∠BAC的正弦值.

    （1）证明见解析（2） 【解析】试题分析：（1）连接OA，要证明AD是⊙O的切线即要证明OA⊥AD，由∠ABC=45°可得出∠AOC=90°，由OC∥AD可得出∠OAD=90°，即证明出OA⊥AD；（2）延长CO交圆O于F，连接BF，要求sin∠BAC即要求sin∠F，因为直径CF，所以∠FBC=90°，所以得出sin∠BAC =sin∠F==. 试题解析： （1）证明：连接OA...

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：填空题

    如图，在平面直角坐标系中，抛物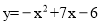线与直线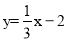相交于点B、C，点P为直线BC上方的抛物线上的一动点， PQ⊥x轴交BC于点Q，PG⊥BC于点G，点M为线段PQ的中点，则线段GM的最大值为_________．

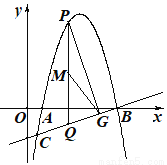
    【解析】设P(x,-x2+7x-6),Q(x, ). 则 ， ∴PQ的最大值是 . ∵点M为线段PQ的中点， ∴ , ∴GM的最大值是 .

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，在△ABC中，∠B=70°，AB=4，BC=6，将△ABC沿图示中的虚线DE剪开，剪下的三角形与原三角形相似的有（ ）

    (1) (2) (3) (4)

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】 图1，∵∠CDE=∠B=70°, ∠C=∠C, ∴△CDE∽△CBA； 图2，∵∠CED=∠B=70°, ∠C=∠C, ∴△CDE∽△CAB； 图3，∵AC的长度不知道，∴无法说明 ,∴△ADE与△ABC不一定相似； 图4，∵∠BDE=∠A=70°, ∠BED=∠C, ∴△BDE∽△BAC； 故选C.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：解答题

    某校为了了解本校七年级学生课外阅读的喜好，随机抽取该校七年级部分学生进行问卷调査（每人只选一种书籍）．如图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：

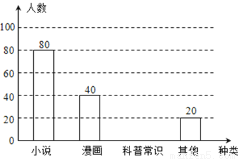
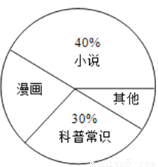
    （1）这次活动一共调查了________名学生；

    （2）在扇形统计图中，“其他”所在扇形的圆心角等于__________度；

    （3）补全条形统计图；

    （4）若该年级有600名学生，请你估计该年级喜欢“科普常识”的学生人数约是__________．

    （1）200 （2）36° （3）如图 （4）180 【解析】分析：（1）根据条形图可知喜欢阅读“小说”的有80人，根据在扇形图中所占比例得出调查学生总数； （2）根据条形图可知阅读“其他”的有20人，根据总人数可求出它在扇形图中所占比例； （3）求出第3组人数画出图形即可； （4）根据喜欢阅读“科普常识”的学生所占比例，即可估计该年级喜欢阅读“科普常识”的人数． ...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：单选题

    一个篮球标价120元，销售时以九折出售，结果仍获利百分之二十，则篮球的进价是（　　）元．

    A. 90 B. 85 C. 80 D. 95

    A 【解析】设篮球的进价为x元/个，则有 （1+20%）x=120×0.9， 解得：x=90， 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型：解答题

    如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于D点，DE⊥AB于E，当AC=6，BC=8时，求DE的长．

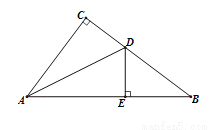
    3 【解析】根据全等三角形的判定和性质、勾股定理即可对本题求解， 【解析】 ∵∠C=90°，DE⊥AB于E， ∴∠ACD =∠AED=90°， ∵AD平分∠BAC交BC于D点， ∴∠CAD =∠EAD， 在Rt△ACD和Rt△AED中， ， ∴△ACD≌△AED（AAS）， ∴ AE=AC=6 ，DE=CD ， ∵BC=8，由勾股定理得...

    查看答案和解析>>

    同步练习册答案