练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

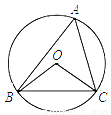
    如图，△ABC是⊙O的内接三角形，若⊙O的半径为2，∠BOC与∠A互补，则BC的长为________．

    【解析】试题分析：过点O作OD⊥BC于D， 则BC＝2BD， ∵△ABC内接于⊙O，∠BAC与∠BOC互补， ∴∠BOC＝2∠A，∠BOC＋∠A＝180°， ∴∠BOC＝120°， ∵OB＝OC， ∴∠OBC＝∠OCB＝ (180°－∠BOC)＝30°， ∵⊙O的半径为2， ∴BD＝OB•cos∠OBC＝2×＝， ∴BC＝2． 故答案为：...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广州市2018学年度七年级（上）数学期末测试卷 题型：单选题

    未来五年，国家将投入8500亿元用于缓解群众“看病难，看病贵”问题．将8500亿元用科学记数法表示为 ( )元

    A. 0.85×1012 B. 8.5×1011 C. 8.5×1012 D. 85×1010

    B 【解析】试题解析：8500亿=8500000000000 故选B.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

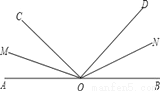
    如图所示，∠AOB是平角，∠AOC=30°，∠BOD=60°，OM，ON分别是∠AOC，∠BOD的平分线，∠MON等于_______度．

    135 【解析】试题分析：∵∠AOC=30°，OM是∠AOC的平分线， ∴∠MOC=∠AOC=×30°=15°， ∵∠BOD=60°，ON是∠BOD的平分线， ∴∠DON=∠BOD=×60°=30°． ∵∠AOB是平角，∠AOC=30°，∠BOD=60°， ∴∠COD=∠AOB-∠AOC-∠BOD=180°-30°-60°=90°． ∵∠MOC=15°，∠...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    下列方程中，是一元一次方程的是 (　 　)

    A. 5x－2y＝9 B. x2－5x＋4＝0 C. 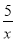＋3＝0 D. 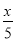－1＝3

    D 【解析】试题解析：A、含有两个未知数，不是一元一次方程； B、未知项的最高次数为2，不是一元一次方程； C、分母中含有未知数，不是一元一次方程； D、符合一元一次方程的定义． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017年中考二模试卷数学试卷 题型：解答题

    先化简，再求值：（1+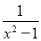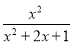）÷，其中x= +1．

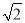    1﹣ 【解析】试题分析：先通分计算括号内的分式的加法，然后把除法转化为乘法，分子、分母因式分解后约分化成最简分式后，把x的值代入化简即可． 试题解析： 【解析】 原式＝（）•， ＝ • ， ＝ ， 当x＝＋1时， 原式＝＝1﹣．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017年中考二模试卷数学试卷 题型：填空题

    分解因式：2x2﹣2=________．

    2（x+1）（x﹣1） 【解析】试题分析： 2x2－2 ＝2(x2－1) ＝2(x＋1)(x－1)． 故答案为2(x＋1)(x－1)．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017年中考二模试卷数学试卷 题型：单选题

    小明在一次射击训练中，共射击10发，成绩如下（单位：环）：8  7  7  8  9  8  7  7  10  8，则中靶8环的频率是（   ）

    A. 0.1                                        B. 0.2                                        C. 0.3                                        D. 0.4

    D 【解析】试题分析：中靶8环的频数为4，所以中靶8环的频率为＝0.4． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市襄城区2016-2017学年度上学期期末考试八年级数学试卷 题型：填空题

    当x=2016时,分式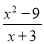的值＝___________.

    2013 【解析】试题解析：当x=2016时，分式=x-3， 则原式=2016-3=2013． 故答案为：2013．

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：解答题

    如图，四边形ABCD为平行四边形，E为BC的中点，连接AE并延长交DC的延长线于点F．

    （1）求证：△ABE≌△FCE；

    （2）过点D作DG⊥AE于点G，H为DG的中点．判断CH与DG的位置关系，并说明理由．

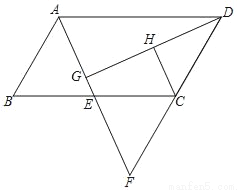
    （1）证明见解析; （2）CH⊥DG．理由见解析. 【解析】（1）根据平行四边形的性质得到两角一边对应相等，利用AAS判定△ABE≌△FCE； （2）易证CH为ΔDGF的中位线，所以CH∥GF，由DG⊥AE可得CH⊥DG． 试题解析：（1）∵四边形为平行四边形 ∴∥， ∴ ∵为的中点 ∴ ∵ ∴△≌△ （2） ∵△≌△ ∴ ...

    查看答案和解析>>

    同步练习册答案