
 在如图的平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在如图的平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:科目:初中数学 来源: 题型:
 如图,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=
如图,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=| 1 |
| 2 |
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 快、慢两车分别从相距240千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车早1小时到达甲地,快、慢两车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.
快、慢两车分别从相距240千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车早1小时到达甲地,快、慢两车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
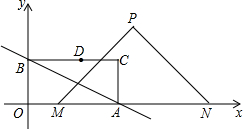 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,甲乙两幢楼之间的距离BD=30m,自甲楼顶端A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为26.6°,求甲、乙楼两幢楼的高度.
如图,甲乙两幢楼之间的距离BD=30m,自甲楼顶端A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为26.6°,求甲、乙楼两幢楼的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com