
如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y= (x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
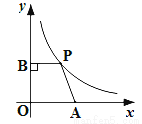
A. 逐渐增大 B. 不变 C. 逐渐减小 D. 先增大后减小
C 【解析】试题分析:设P(a,),直角梯形APBO的面积=(OA+a)×=+,OA为定值,所以直角梯形APBO的面积随x的增大而减小,故答案选C.科目:初中数学 来源:北京101中学2017-2018学年上学期初中七年级期末考试数学试卷 题型:解答题
阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数: 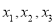 ,称为数列
,称为数列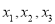 .计算
.计算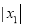 ,
, 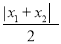 ,
, 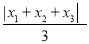 将这三个数的最小值称为数列
将这三个数的最小值称为数列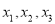 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为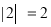 ,
, 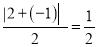 ,
, 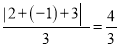 ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为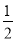 .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为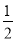 ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为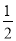 .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
(1)(2);-3,2,-4或2,-3,-4(3)11或4或7或10 【解析】试题分析:(1)根据上述材料给出的方法计算其相应的价值即可; (2)按照三个数不同的顺序排列算出价值,由计算可以看出,要求得这些数列的价值的最小值;只有当前两个数的和的绝对值最小,最小只能为|-3+2|=1,由此得出答案即可; (3)分情况算出对应的数值,建立方程求得a的数值即可. 试题解析::(1)因为...查看答案和解析>>
科目:初中数学 来源:陕西省西安市师大2017-2018学年初三期中考试数学试卷 题型:填空题
等腰三角形的底角为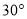 ,底边长为
,底边长为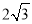 ,则腰长为__________.
,则腰长为__________.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
计算(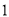 )(
)(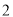 ),并解(
),并解(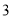 )(
)(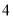 )两个方程(每题
)两个方程(每题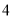 分,共
分,共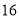 分)
分)
(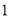 )
)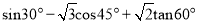 .
.
(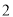 )
)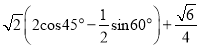 .
.
(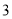 )
)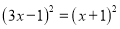 .
.
(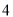 )
)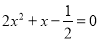 .
.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:填空题
在平面直角坐标系中, 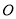 为原点,
为原点, 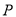 点的坐标为
点的坐标为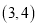 ,
, 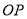 与
与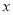 轴的夹角为
轴的夹角为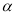 ,则
,则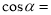 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:单选题
在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A. 16个 B. 15个 C. 13个 D. 12个
D 【解析】试题分析:由摸到红球的频率稳定在25%附近得出口袋中得到红色球的概率,进而求出白球个数即可. 【解析】 设白球个数为:x个, ∵摸到红色球的频率稳定在25%左右, ∴口袋中得到红色球的概率为25%, ∴=, 解得:x=12, 故白球的个数为12个. 故选:D.查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
考古学家从幼发拉底河附近的一座寺庙里,发掘出数千块泥板书,他们从泥板书中发现美索不达米亚的祭祀已经知道平方表的用法,并能够利用平方表算出任意两个自然数的乘积.
例如:计算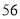 乘以
乘以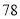 ,祭祀们会按下面的流程操作:
,祭祀们会按下面的流程操作:
第一步: 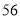 加上
加上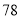 ,将和除以
,将和除以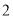 得
得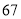 ;
;
第二步: 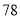 减去
减去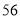 ,将差除以
,将差除以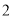 得
得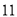 ;
;
第三步:查平方表,得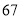 的平方是
的平方是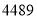 ;
;
第四步:查平方表,得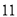 的平方是
的平方是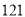 ;
;
第五步: 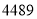 减去
减去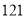 ,得到答案
,得到答案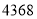 .
.
于是他们便得出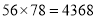 .
.
请你利用所学的代数知识,设两个自然数分别为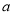 、
、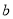 ,对泥板书计算两个自然数乘积的合理性做出解释.
,对泥板书计算两个自然数乘积的合理性做出解释.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型:解答题
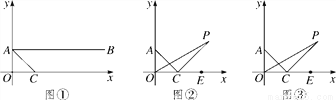
如图①,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB.
(1)求证:∠OAC=∠OCA;
(2)如图②,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC=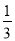 ∠AOC,∠PCE=
∠AOC,∠PCE=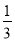 ∠ACE,求∠P的大小;
∠ACE,求∠P的大小;
(3)如图③,在(2)中,若射线OP、CP满足∠POC=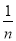 ∠AOC,∠PCE=
∠AOC,∠PCE=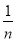 ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).
∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com