
实验初中组织了“英语手抄报”征集活动,现从中随机抽取部分作品,按A、B、C、D四个等级进行评价,并根据统计结果绘制了如下两幅不完整的统计图.
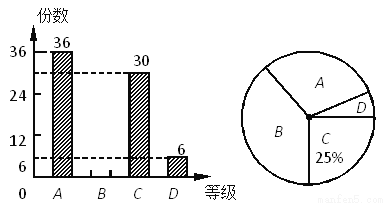
(1)抽取了_份作品;
(2)此次抽取的作品中等级为B的作品有_份,并补全条形统计图;
(3)若该校共征集到600份作品,请估计等级为A的作品约有多少份?
(1)120 ;(2)48,画图见解析;(3)等级为A的作品约有180份. 【解析】试题分析:(1)用C等级份数除以C等级所占的百分比,可得抽取的数量; (2)用(1)中所求总份数减去A、C、D三等级数量即可得到B等级作品数,并补全统计图; (3)利用样本估计总体,将样本中A等级所占比例乘以600,可估计A等级数量. 【解析】 (1)根据题意,共抽取作品30÷25%=12...科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:填空题
已知点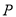 的坐标为
的坐标为 ,则点
,则点 到
到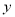 轴的距离为__________.
轴的距离为__________.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:解答题
已知:如图,在?ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:单选题
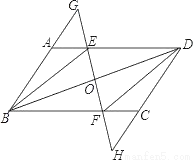
如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A. 5 B. 6 C. 8 D. 10
C 【解析】因为AB=AC,AD是∠BAC的平分线,所以BC=2BD. 因为BD=4,所以BC=2BD=2×4=8. 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017届九年级上学期期末考试数学试卷 题型:解答题
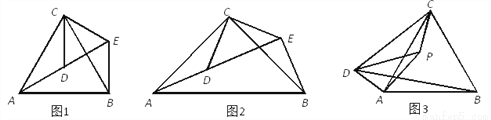
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则:
①∠BEC=_°;②线段AD、BE之间的数量关系是_.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017届九年级上学期期末考试数学试卷 题型:填空题
如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(-1,0),若将线段BA绕点B顺时针旋转90°得到线段BA',则点A'的坐标为___.
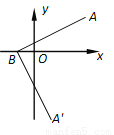
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017届九年级上学期期末考试数学试卷 题型:填空题
函数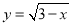 的自变量x的取值范围是_.
的自变量x的取值范围是_.
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:解答题
(1)计算: 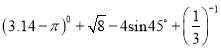 ;
;
(2)解方程: 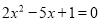 .
.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
某公司有A产品40件,B产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润 (元) 如下表所示:
A产品的利润/元 | B产品的利润/元 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1) 设分配给甲店A产品x件,这家公司卖出这100件产品的总利润为W (元),求W关于x的函数关系式,并求出x的取值范围;
(2) 若要求总利润不低于17560元;有多少种不同的分配方案? 并将各种方案设计出来;
(3) 为了促销,公司决定仅对甲店A产品让利销售,每件让利a元,但让利后A产品的每件利润仍高于甲店B产品的每件利润.甲店的B产品以及乙店的A,B产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
(1)10≤x≤40; (2)详见解析;(3)当x=10时,利润最大. 【解析】试题分析:(1)分配给甲店A型产品x件,则分配给甲店B型产品(70-x)件,分配给乙店A型产品(40-x)件,分配给乙店B型产品(x-10)件,根据总利润等于各利润之和进行求解;根据x≥0,40-x≥0,30-(40-x)≥0可以求出取值范围;(2)、根据W≤17560得到x的取值范围,和(1)中的取值范围得到x...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com