
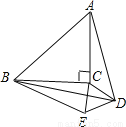
如图,以等腰直角三角形ABC的斜边AB为边作等边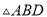 ,连接DC,以DC当边作等边
,连接DC,以DC当边作等边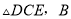 、E在C、D的同侧,若
、E在C、D的同侧,若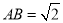 ,求BE的长.
,求BE的长.
科目:初中数学 来源:湖南省2018届九年级上学期期末考试数学试卷 题型:填空题
三角形的周长为76cm,则它的三条中位线组成的三角形的周长是_________cm.
38 【解析】 由中位线的性质可得:DE=BC,DF=AC,EF=AB, ∴C△DEF=C△ABC=38cm. 故答案为38.查看答案和解析>>
科目:初中数学 来源:江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
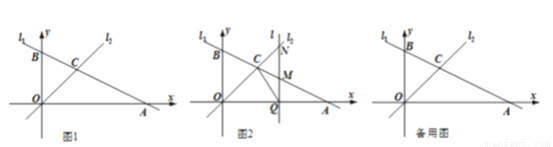
如图1,直线 与坐标轴分别交于点
与坐标轴分别交于点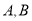 ,与直线
,与直线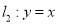 交于点
交于点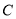 .
.
(1) 求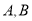 两点的坐标;
两点的坐标;
(2) 求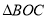 的面积;
的面积;
(3)如图2,若有一条垂直于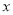 轴的直线
轴的直线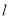 以每秒1个单位的速度从点
以每秒1个单位的速度从点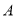 出发沿射线
出发沿射线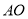 方向作匀速滑动,分别交直线
方向作匀速滑动,分别交直线 及
及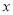 轴于点
轴于点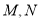 和
和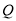 .设运动时间为
.设运动时间为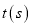 ,连接
,连接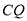 .
.
① 当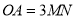 时,求
时,求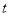 的值;
的值;
② 试探究在坐标平面内是否存在点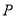 ,使得以
,使得以 、
、 、
、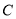 、
、 为顶点的四边形构成菱形?若存在,请直接写出
为顶点的四边形构成菱形?若存在,请直接写出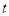 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
据统计:我国微信用户数量已突破8.87亿人,近似数8.87亿精确到______位.
百万 【解析】【解析】 8.87亿精确到百万位.故答案为:百万.查看答案和解析>>
科目:初中数学 来源:江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列说法中正确的是( )
A. 掷一枚质地均匀的硬币10次,一定会有5次正面向上
B. “ x2<0(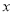 是实数)”是随机事件
是实数)”是随机事件
C. “抛掷1枚骰子,向上的点数为6”是随机事件
D. “打开电视,正在播放《新闻联播》”是必然事件
C 【解析】【解析】 A、随机事件,故选项A错误; B、不可能事件,故选项B错误; C、正确; D、随机事件,故选项D错误. 故选C.查看答案和解析>>
科目:初中数学 来源:云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
一次测验共出5道题,做对一题得一分,已知26人的平均分不少于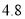 分,最低的得3分,至少有3人得4分,则得5分的有______ 人
分,最低的得3分,至少有3人得4分,则得5分的有______ 人
查看答案和解析>>
科目:初中数学 来源:云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
钟表上2时15分,时针与分针的夹角是
A. 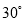 B.
B. 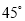 C.
C. 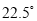 D.
D. 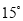
查看答案和解析>>
科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:填空题
如图,将长方形纸片的一角折叠,使顶点A落在A′处,EF为折痕,再将另一角折叠,使顶点B落在EA′上的B′点处,折痕为EG,则∠FEG等于________度.
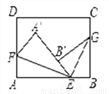
查看答案和解析>>
科目:初中数学 来源:云南省双柏县2017-2018学年八年级上期期末数学试卷 题型:解答题
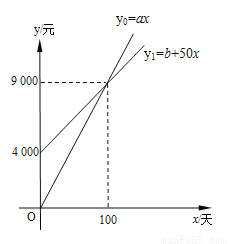
国家推行“节能减排,低碳经济”政策后,某企业推出一种“CNG”改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0,y1(元)与正常运营时间x(天)之间分别满足关系式:y0=ax,y1=b+50x,图象如图所示.
(1)每辆车改装前每天的燃料费a= 元,每辆车的改装费b= 元,正常运营时间 天后,就可以从节省的燃料费中收回改装成本;
(2)某出租汽车公司一次性改装了100辆出租车,因而正常运行多少天后共节省燃料费40万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com