练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE.

    (1)求证：CE＝CF；

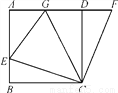
    (2)若点G在AD上，且∠GCE＝45°，则GE＝BE＋GD成立吗？为什么？

    (1)证明见解析(2)GE＝BE＋GD成立 【解析】试题分析：（1）由DF=BE，四边形ABCD为正方形可证△CEB≌△CFD，从而证出CE=CF； （2）由（1）得CE=CF，∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，又∠GCE=45°，所以可得∠GCE=∠GCF，故可证得△ECG≌△FCG，即EG=FG=GD+DF．又因为DF=BE，所以可证出GE=BE...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版七年级下册 第1-3章 综合测试卷 题型：单选题

    体育课上，七年级某班49名同学在操场上练习正方形方队，他们站成7×7方队，每横队7人，每纵队7人，小敏在第2纵队的排头，记为（1，2），小娟在第5纵队的队尾，则小娟的位置应记为（    ）

    A. （6，5） B. （5，6） C. （5，7） D. （7，5）

    D 【解析】【解析】 小娟在第5纵队的队尾，则小娟的位置应记为（7，5）．故选D．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：解答题

    已知反比例函数y=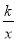的图象与一次函数y=kx+m的图象相交于点A（2，1）．

    （1）分别求出这两个函数的解析式；

    （2）当x取什么范围时，反比例函数值大于0；

    （3）若一次函数与反比例函数另一交点为B，且纵坐标为﹣4，当x取什么范围时，反比例函数值大于一次函数的值；

    （4）试判断点P（﹣1，5）关于x轴的对称点P′是否在一次函数y=kx+m的图象上．

    （1）y=，y=2x﹣3；（2）x＞0；（3）x＜﹣0.5或0＜x＜2；（4）点P′在直线上． 【解析】试题分析：（1）根据题意，反比例函数y=的图象过点A（2，1），可求得k的值，进而可得解析式；一次函数y=kx+m的图象过点A（2，1），代入求得m的值，从而得出一次函数的解析式；（2）根据（1）中求得的解析式，当y＞0时，解得对应x的取值即可； （3）由题意可知，反比例函数值大于一...

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：填空题

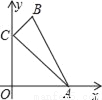
    如图，在平面直角坐标系中，点A是x轴正半轴上的一个动点，点C是y轴正半轴上的点，BC⊥AC于点C．已知AC=8，BC=3．

    （1）线段AC的中点到原点的距离是_____；

    （2）点B到原点的最大距离是_____．

    4 9 【解析】(1)因为∠AOC=90°,AC=8,所以线段AC的中点到原点的距离是: ,AC=4, (2)取AC的中点E,连接BE,OE,OB, 因为∠AOC=90°,AC=8,所以OE=CE=,AC=4, 因为BC⊥AC,BC=3, 所以BE=5, 若点O,E,B不在一条直线上,则OB

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：单选题

    如图，矩形ABCD中，已知点M是线段AB的黄金分割点，且AM＞BM，AD=AM，FB=BM，EF和GM把矩形ABCD分成四个小矩形，其面积分别用S1，S2，S3，S4表示，EF与MG相交与点N，则以下结论正确的有（　　）

    ①N是GM的黄金分割点 ②S1=S4③．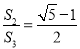

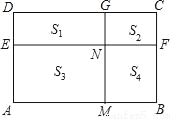
    A. ①② B. ①③ C. ③ D. ①②③

    A 【解析】因为四边形ABCD是矩形,AM=AD,BM=BF, 所以四边形AMGD,四边形BMNF都是正方形, 所以AM=AD=MG=BC,MB-BF=MN=FN, 因为点M是线段AB的黄金分割点,AM>BM, 所以, 所以, 所以,故②正确, 所以, 所以N是GM的黄金分割点,故①正确, 因为, 因为, 所以,故③错误, ...

    查看答案和解析>>

    科目：初中数学 来源：2018届九年级中考数学专题复习同步练习题：平行四边形 题型：填空题

    如图，正方形ABCO的顶点C、A分别在x轴、y轴上，BC是菱形BDCE的对角线，若∠D=60°，BC=2，则点D的坐标是_____．

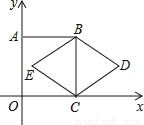
    （2+，1）． 【解析】试题解析：过点D作DG⊥BC于点G， ∵四边形BDCE是菱形， ∴BD=CD． ∵BC=2，∠D=60°， ∴△BCD是等边三角形， ∴BD=BC=CD=2， ∴CG=1，GD=CD•sin60°=2×=， ∴D（2+，1）．

    查看答案和解析>>

    科目：初中数学 来源：2018届九年级中考数学专题复习同步练习题：平行四边形 题型：单选题

    如图，把矩形纸片ABCD沿对角线BD折叠，设重叠部分为△EBD，则下列说法错误的是(　　)

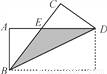
    A. AB＝CD B. ∠BAE＝∠DCE C. EB＝ED D. ∠ABE一定等于30°

    D 【解析】试题分析：根据ABCD为矩形，所以∠BAE=∠DCE，AB=CD，再由对顶角相等可得∠AEB=∠CED，所以△AEB≌△CED，就可以得出BE=DE，由此判断即可． 【解析】 ∵四边形ABCD为矩形 ∴∠BAE=∠DCE，AB=CD，故A、B选项正确； 在△AEB和△CED中， ， ∴△AEB≌△CED（AAS）， ∴BE=DE，故C正确； ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2018届九年级上学期期末考试数学试卷 题型：解答题

    计算：

    （1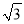）()2－|-6|＋(－2)0； （2） (2x＋1)(2x－1)－4(x＋1)2．

    （1）-2 ；（2） 【解析】试题分析：（1）先分别计算乘方、0次幂，化简绝对值，然后再进行加减运算即可； （2）先分别利用平方差公式，完全平方公式进行展开，然后再合并同类项即可. 试题解析：（1）原式= 3-6+1 = -2 ； （2）原式===.

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第三章 图形的平移与旋转 单元检测卷 题型：单选题

    在下列图形中，是中心对称图形的是(     )

    A. B. C. D.

    C 【解析】试题分析：A、旋转180°后不能与自身重合，不是中心对称图形； B、旋转180°后不能与自身重合，不是中心对称图形； C、旋转180°后能与自身重合，是中心对称图形； D、旋转180°后不能与自身重合，不是中心对称图形． 故选C．

    查看答案和解析>>

    同步练习册答案