
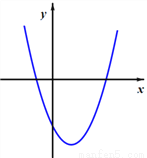
二次函数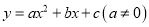 的图象如图所示,
的图象如图所示, 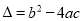 ,则下列四个选项正确的是( )
,则下列四个选项正确的是( )
A. 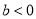 ,
, 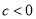 ,
, 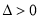 B.
B. 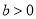 ,
, 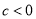 ,
, 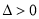
C. 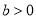 ,
, 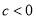 ,
, 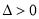 D.
D. 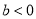 ,
, 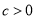 ,
, 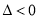
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
解方程: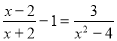 .
.
查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:单选题
甲看乙的方向是南偏西26 ,则乙看甲的方向是( )
,则乙看甲的方向是( )
A. 南偏东64 B. 北偏西64
B. 北偏西64 C. 北偏东26
C. 北偏东26 D. 北偏西26
D. 北偏西26
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:解答题
计算: 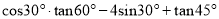 .
.
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:填空题
已知点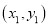 ,
, 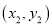 在反比例函数
在反比例函数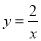 上,当
上,当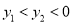 时,
时, 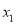 ,
, 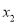 的大小关系是____________.
的大小关系是____________.
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:解答题
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
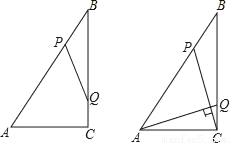
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
(1) t=1或 ;(2) 【解析】试题分析: (1)由∠B是△BPQ与△ABC的公共角,可知,若两三角形相似,存在两种情况:①△BPQ∽△BAC;②△BPQ∽△BCA;分这两种情况结合相似三角形的性质和题意即可解得对应的t的值; (2)如图1,过P作PM⊥BC于点M,AQ,CP交于点N,由题意可知:当AQ⊥CP时,△ACQ∽△CMP,由相似三角形的性质列出比例式即可解得对应的t...查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,AD⊥BC于点D,则△ACD与△ABC的面积比为_________
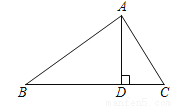
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3s后,两点相距18个单位长度.已知点B的速度是点A的速度的5倍(速度单位:单位长度/s).
(1)求出点A、点B运动的速度,并在数轴上标出A,B两点从原点出发运动3s时的位置;
(2)若A,B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)当A,B两点从(2)中的位置继续以原来的速度沿数轴向左运动的同时,另一点C从原点位置也向点A运动,当遇到点A后,立即返回向点B运动,遇到点B后又立即返回向点A运动,如此往返,直到点B追上点A时,点C立即停止运动.若点C一直以8个单位长度/s的速度匀速运动,则点C从开始运动到停止运动,行驶的路程是多少个单位长度?
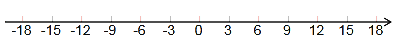
查看答案和解析>>
科目:初中数学 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:填空题
如图,等边三角形ABC的外接圆⊙O的半径OA的长为2,则其内切圆半径的长为__________.
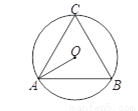
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com