名师点拨卷系列答案科目：初中数学 来源：2018年吉林省中考数学一模试卷 题型：单选题
如图，在Rt△ABC中，∠A＝30°，BC＝1，点D，E分别是直角边BC，AC的中点，则DE的长为( )
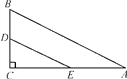
A. 1 B. 2 C.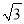 
D. 1＋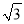
查看答案和解析>>
科目：初中数学 来源：江西省赣州市心城区六校联盟2018届九年级下学期联考数学试卷 题型：填空题
已知抛物线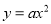
与线段AB无公共点，且A（-2，-1），B（-1，-2），则a的取值范围是___________.
查看答案和解析>>
科目：初中数学 来源：2018年湖北省武汉市中考数学一模试卷 题型：解答题
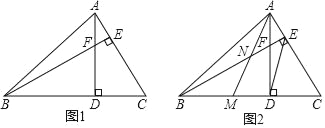
如图1，在锐角△ABC中，∠ABC=45°，高线AD、BE相交于点F．
（1）判断BF与AC的数量关系并说明理由；
（2）如图2，将△ACD沿线段AD对折，点C落在BD上的点M，AM与BE相交于点N，当DE∥AM时，判断NE与AC的数量关系并说明理由．
【答案】（1）BF=AC，理由见解析；（2）NE=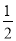
AC，理由见解析.
【解析】试题分析：（1）如图1，证明△ADC≌△BDF（AAS），可得BF=AC；
（2）如图2，由折叠得：MD=DC，先根据三角形中位线的推论可得：AE=EC，由线段垂直平分线的性质得：AB=BC，则∠ABE=∠CBE，结合（1）得：△BDF≌△ADM，则∠DBF=∠MAD，最后证明∠ANE=∠NAE=45°，得AE=EN，所以EN=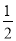
AC．
试题解析：
（1）BF=AC，理由是：
如图1，∵AD⊥BC，BE⊥AC，
∴∠ADB=∠AEF=90°，
∵∠ABC=45°，
∴△ABD是等腰直角三角形，
∴AD=BD，
∵∠AFE=∠BFD，
∴∠DAC=∠EBC，
在△ADC和△BDF中，
∵
，
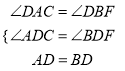∴△ADC≌△BDF（AAS），
∴BF=AC；
（2）NE=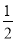
AC，理由是：
如图2，由折叠得：MD=DC，
∵DE∥AM，
∴AE=EC，
∵BE⊥AC，
∴AB=BC，
∴∠ABE=∠CBE，
由（1）得：△ADC≌△BDF，
∵△ADC≌△ADM，
∴△BDF≌△ADM，
∴∠DBF=∠MAD，
∵∠DBA=∠BAD=45°，
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD，
即∠ABE=∠BAN，
∵∠ANE=∠ABE+∠BAN=2∠ABE，
∠NAE=2∠NAD=2∠CBE，
∴∠ANE=∠NAE=45°，
∴AE=EN，
∴EN=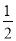
AC．
【题型】解答题
【结束】
19
某校学生会决定从三明学生会干事中选拔一名干事当学生会主席，对甲、乙、丙三名候选人进行了笔试和面试，三人的测试成绩如下表所示：
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
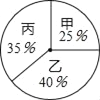
根据录用程序，学校组织200名学生采用投票推荐的方式，对三人进行民主测评，三人得票率如扇形统计图所示（没有弃权，每位同学只能推荐1人），每得1票记1分．
（1）分别计算三人民主评议的得分；
（2）根据实际需要，学校将笔试、面试、民主评议三项得分按3：3：4的比例确定个人成绩，三人中谁会当选学生会主席？
查看答案和解析>>
科目：初中数学 来源：2018年湖北省武汉市中考数学一模试卷 题型：单选题
同时使分式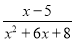
有意义，又使分式
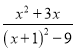无意义的x的取值范围是（ ）
A. x≠﹣4且x≠﹣2 B. x=﹣4，或x=2 C. x=﹣4 D. x=2
查看答案和解析>>
科目：初中数学 来源：2018年湖北省黄石市中考数学一模试卷 题型：解答题
已知：关于x的方程x2+2x﹣k=0有两个不相等的实数根．
（1）求k的取值范围；
（2）若α，β是这个方程的两个实数根，求：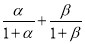 
的值；
（3）根据（2）的结果你能得出什么结论？
查看答案和解析>>
科目：初中数学 来源：2017-2018学年山西农大附中九年级上学期期中数学试卷 题型：单选题
用配方法解一元二次方程x2﹣4x=5时，此方程可变形为（ ）
A. （x+2）2=1 B. （x﹣2）2=1 C. （x+2）2=9 D. （x﹣2）2=9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=_____．