
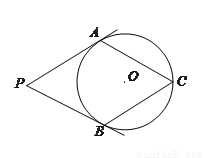
如图, 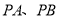 分别与
分别与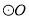 相切于
相切于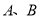 两点,点
两点,点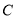 在
在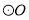 上,∠P=60º,
上,∠P=60º,
(1)求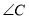 的度数;
的度数;
(2)若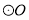 半径为1,求
半径为1,求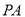 的长.
的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:黑龙江省大庆市2016-2017下学期初一期末数学试卷 题型:填空题
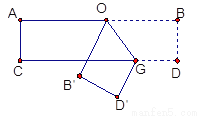
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°, 则∠B′OG的度数为__________.
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
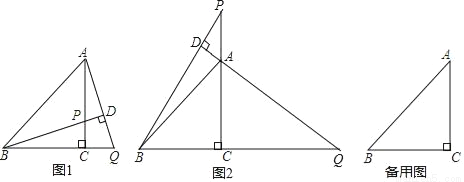
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立? (填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA= 度时,存在AQ=2BD,说明理由.
(1)证明见解析;(2)(2)成立,理由见解析;(3)当∠DBA=22.5°时,存在AQ=2BD,理由见解析. 【解析】试题分析:(1)首先根据内角和定理得出∠DAP=∠CBP,进而得出 △ACQ≌△BCP即可得出答案; (2)延长BA交PQ于H,由于 得到 推出△AQC≌△BPC(ASA),即可得出结论; (3)当时,存在根据等腰三角形的性质得到BP=2BD,通过△PBC≌△AC...查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列等式从左到右的变形,属于因式分解的是( )
A. 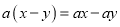 B.
B. 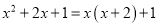
C. 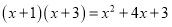 D.
D. 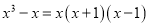
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
已知△ABC中, 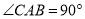 ,
, 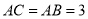 ,△CDE中,
,△CDE中, 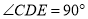 ,CD=DE=5,
,CD=DE=5,
连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若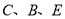 三点共线,
三点共线, 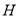 为
为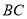 中点.
中点.
①直接指出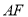 与
与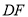 的关系______________;
的关系______________;
②直接指出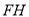 的长度______________;
的长度______________;
(2)将图(1)中的△CDE绕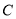 点逆时针旋转
点逆时针旋转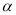 (如图2,
(如图2, 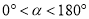 ),试确定
),试确定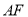 与
与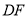 的关系,并说明理由;
的关系,并说明理由;
(3)在(2)中,若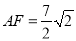 ,请直接指出点
,请直接指出点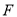 所经历的路径长.
所经历的路径长.
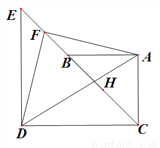
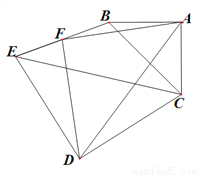
图1 图2
(1)①, ,②;(2), ,理由见解析;(3)或 【解析】试题分析:(1)①如图,过点F M⊥CD于M,FN⊥AC交CA的延长线于点N,根据已知条件易证四边形FMCN为正方形,可得FN=FM,再证△FNA≌△FMD,即可得∠NFA=∠DFM,DF=AF,所以∠NFA+∠AFM=∠DFM+∠AFM=∠DFA=90°,即可证得;②根据勾股定理求得BC=,EC=5 ,因为中点,F为BE的中点,可...查看答案和解析>>
科目:初中数学 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:填空题
在平面直角坐标系中,将点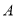 (2,-1)绕原点
(2,-1)绕原点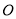 旋转
旋转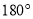 后,得到的对应点
后,得到的对应点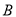 的坐标为___________.
的坐标为___________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:单选题
下列事件属于随机事件的是( )
A. 任意画一个三角形,其内角和为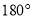 B. 经过有交通信号灯的路口,遇到红灯
B. 经过有交通信号灯的路口,遇到红灯
C. 掷一次骰子,向上一面点数是7 D. 明天的太阳从东方升起
B 【解析】选项A、D是必然事件;选项C是不可能事件;选项B是随机事件.故选B.查看答案和解析>>
科目:初中数学 来源:江苏省宿迁市2017-2018学年上学期第二次形成性测试七年级数学试卷 题型:填空题
一个两位数,设它的个位上的数字为x,十位上的数字比个位上的数字大1,这个两位数的2倍加2等于66,根据题意所列方程是_____.
2〔10(x+1) +x〕+2=66 【解析】【解析】 根据题意得:2〔10(x+1) +x〕+2=66.故答案为:2〔10(x+1) +x〕+2=66.查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
阅读下面的文字,完成后面的问题:
我们知道: 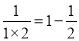 ,
, 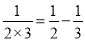 ,
, 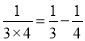
那么(1)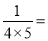 _____________;
_____________;  ________________;
________________;
(2)用含有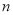 的等式表示你发现的规律________________________;
的等式表示你发现的规律________________________;
(3)如果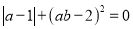 ,求
,求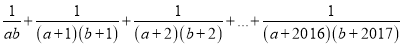 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com