
��֪��ABC�У� 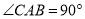 ��
�� 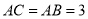 ����CDE��
����CDE�� 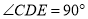 ��CD=DE=5,
��CD=DE=5,
���ӽ�BE��ȡBE�е�F,����AF��DF.
��1����ͼ1����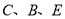 ���㹲�ߣ�
���㹲�ߣ� 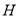 Ϊ
Ϊ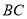 �е�.
�е�.
��ֱ��ָ��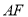 ��
��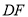 �Ĺ�ϵ______________��
�Ĺ�ϵ______________��
��ֱ��ָ��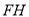 �ij���______________��
�ij���______________��
��2����ͼ��1���еġ�CDE��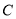 ����ʱ����ת
����ʱ����ת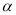 ����ͼ2��
����ͼ2�� 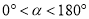 ������ȷ��
������ȷ��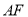 ��
��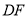 �Ĺ�ϵ����˵�����ɣ�
�Ĺ�ϵ����˵�����ɣ�
��3���ڣ�2���У���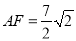 ����ֱ��ָ����
����ֱ��ָ����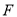 ��������·����.
��������·����.
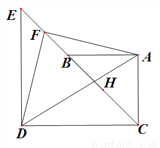
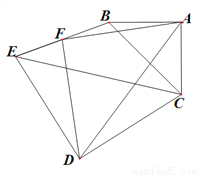
ͼ1 ͼ2
��1���٣� ���ڣ���2���� �����ɼ���������3���� �������������������1������ͼ������F M��CD��M��FN��AC��CA���ӳ����ڵ�N��������֪������֤�ı���FMCNΪ�����Σ��ɵ�FN=FM����֤��FNA�ա�FMD�����ɵá�NFA=��DFM��DF=AF�����ԡ�NFA+��AFM=��DFM+��AFM=��DFA=90�㣬����֤�ã��ڸ��ݹ��ɶ������BC=��EC=5 ����Ϊ�е㣬FΪBE���е㣬��...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������ʡ������2016-2017��ѧ�ڳ�һ��ĩ��ѧ�Ծ� ���ͣ������
��֪���������ε��ڽǺ�Ϊ180�㣬�����ö�����й�ijһ��ĶԽ���������Ѱ�������ڽǺ͵Ĺ�ʽ��

������ͼ��ʾ��һ���ı��ο��Էֳ�2�������Σ������ı��ε��ڽǺ�Ϊ360�ȣ�һ������ο��Էֳ�3�������Σ���������ε��ڽǺ�Ϊ540�ȣ��������˹���n���ε��ڽǺ�Ϊ________�ȣ�
��n-2����180�� ���������������� ���������ڽǺ� �ı����ڽǺ� ������ڽǺ� �������ڽǺ� 180���1 180���2 180���3 180���4 ���n����ijһ����ɻ���n��3�����Խ��ߣ���n���η�Ϊ��n��2���������Σ��⣨n��2���������ε��ڽǺ�֮�;͵���n���ε��ڽǺͣ�����n��2��•180�㣮�ʴ�Ϊ����n��2��•180�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ������У2017-2018ѧ�����꼶�ϲ���ĩ��ѧ���������ѧ�Ծ� ���ͣ���ѡ��
��֪|x|=3��|y|=2����xy��0����x+y��ֵ�ǣ� ��
A. -5��5 B. -1 C. 1 D. -1��1
D ����������xy��0����x��y��ţ� �ߣ� ����x=��3��y=��2�� ��x=3��y=-2ʱ��x+y=1 ��x=-3��y=2ʱ��x+y=-1 ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ʽ�֡�������
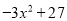 =________��
=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
���и�ʽ������ȷ���ǣ� ��
A. 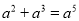 B.
B. 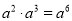 C.
C. 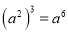 D.
D. 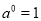
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����人�о��꼶Ԫ�����ϲ�����ѧ�Ծ� ���ͣ������
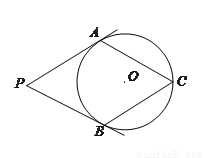
��ͼ�� 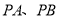 �ֱ���
�ֱ���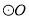 ������
������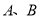 ���㣬��
���㣬��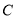 ��
��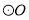 �ϣ���P=60º��
�ϣ���P=60º��
��1����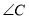 �Ķ�����
�Ķ�����
��2����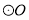 �뾶Ϊ1����
�뾶Ϊ1����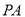 �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����人�о��꼶Ԫ�����ϲ�����ѧ�Ծ� ���ͣ������
ij����������ǰÿ���ۼ�Ϊ20Ԫ�������ۼ�Ϊ12.8Ԫ����ÿ����ص���ƽ���½���Ϊ___________.
20% ����������ÿ�ν��۵İٷ���Ϊx���������⣬���з���20��1-x��2=12.8�����x=0.2��x=1.8����ȥ������ÿ�ν��۵İٷ���Ϊ20%.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��Ǩ��2017-2018ѧ����ѧ�ڵڶ����γ��Բ������꼶��ѧ�Ծ� ���ͣ������
�����з��̣�
(1) 0.5 x ��0.7��6.5��1.3 x�� (2) 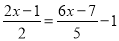 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ���������2018����꼶��ѧ����ĩ���в�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���ACB��90�㣬CD��AB���ϵĸߣ����BD =4��CD=6����ô �ǣ� ��
�ǣ� ��

A. 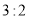 B.
B. 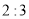 C.
C. 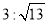 D.
D. 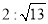
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com