练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若(x-2)0=1，则( )

    A．x≠0 B．x≥2 C．x≤2 D．x≠2

    D 【解析】 零次幂的底数不等于零，让底数不等于零即可．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册 同步测试 1.3 同底数幂的除法 题型：单选题

    下列计算正确的是（ ）

    A. （a5）2=a10 B. x16÷x4=x4 C. 2a2+3a2=6a4 D. b3•b3=2b3

    A 【解析】试题分析：根据幂的乘方底数不变指数相乘，同底数幂的除法底数不变指数相减，合并同类项系数相加字母及指数不变，同底数幂的乘法底数不变指数相加，可得答案．A、幂的乘方底数不变指数相乘，故A正确； B、同底数幂的除法底数不变指数相减，故B错误；C、合并同类项系数相加字母及指数不变，故C错误； D、同底数幂的乘法底数不变指数相加，故D错误；

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册 同步测试 1.3 同底数幂的除法 题型：单选题

    （π﹣3.14）0的相反数是（　　）

    A. 3.14﹣π B. 0 C. 1 D. ﹣1

    D 【解析】试题分析：（π﹣3.14）0的相反数是：﹣1．故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册 同步测试 1.3 同底数幂的除法 题型：单选题

    下列运算正确的是（　　）

    A. a8÷a2=a4 B. a5﹣（﹣a）2=﹣a3 C. a3•（﹣a）2=a5 D. 5a+3b=8ab

    C 【解析】试题分析：A .a8÷a2=a8-2=a6≠a4，故本选项错误； B. a5﹣（﹣a）2=﹣a3，本选项错误； C. a3•（﹣a）2=a5，正确； D. 5a+3b=8ab，本选项错误. 故选C. 考点: 整式的运算.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册1.3.1同底数幂的除法 练习题 题型：填空题

    0.00000123用科学计数法表示为__________：．

    1.23×106 【解析】∵从左起的第一个非0数1前面有6个0，∴0.00000123=1.23×106.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.3.1 平行线的性质 同步练习 题型：解答题

    如图是某次考古发掘出的一个四边形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°,已知在四边形中,AD∥BC,请你帮助工作人员求出另外两个角的度数.

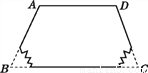
    ∠B=65°，∠C=70° 【解析】试题分析：本题主要利用两直线平行，同旁内角互补进行做题． 试题解析：【解析】 因为AD∥BC(已知)，所以∠A+∠B=180°，∠C+∠D=180°(两直线平行，同旁内角互补)．所以∠B=180°-∠A=180°-115°=65°，∠C=180°-∠D=180°-110°=70°．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.3.1 平行线的性质 同步练习 题型：单选题

    如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点,这时,∠ABC的度数是(　　)

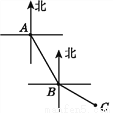
    A. 120° B. 135° C. 150° D. 160°

    C 【解析】如图，先根据题意可得：∠1＝30°，∠2＝60°，再根据平行线的性质可得∠4＝∠1＝30°，再根据∠2和∠3互余可算出∠3的度数，进而求出∠ABC＝∠4＋∠3＋∠FBD＝150°．

    查看答案和解析>>

    科目：初中数学 来源：北师大版 七年级数学下册 第一章　整式的乘除 单项式与单项式相乘 专题练习题 含答案 题型：填空题

    计算下列各题，结果用科学记数法表示：

    (1)(－3×105)×(5×103)＝__________；

    (2)(8×106)×(5×103)×(2×102)＝________；

    (3)(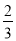－×10)3×(1.5×103)4＝___________.

    －1.5×109 8×1012 －1.5×1015 【解析】试题分析：科学计数法是指，且n为原数的整数位数减一．首先将系数进行相乘，然后根据同底数幂的乘法计算法则进行计算，最后转化为科学计数法形式．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型：解答题

    如图，△ABC与△A′B′C′是以点O为位似中心的位似图形，它们的顶点都在正方形网格的格点上．

    (1)画出位似中心O；

    (2)△ABC与△A′B′C′的相似比为__________，面积比为__________.

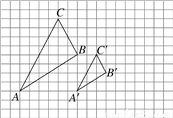
    （1）作图见解析；（2）2∶1；4∶1. 【解析】（1）根据位似的性质，延长AA′、BB′、CC′，则它们的交点即为位似中心O； （2）根据位似的性质得到AB：A′B′=OA：OA′=2：1，则△ABC与△A′B′C′的相似比为2：1，然后根据相似三角形的性质得到它们面积的比． 解：(1)如图，点O为位似中心； (2)因为AB:A′B′=OA:OA′=12:6=2:1， ...

    查看答案和解析>>

    同步练习册答案