练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知x=3﹣k，y=2+k，则y与x的关系是（　　）

    A. y=x﹣5 B. x+y=1 C. x﹣y=1 D. x+y=5

    D 【解析】∵x=3﹣k，y=2+k， ∴x+y=3﹣k+2+k=5． 故选：D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下5.3.1 等腰三角形的性质 同步练习 题型：解答题

    如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．

    证明见解析. 【解析】试题分析：首先根据AB=AC=AD，可得∠C=∠ABC，∠D=∠ABD，∠ABC=∠CBD+∠D；然后根据AD∥BC，可得∠CBD=∠D，据此判断出∠ABC=2∠D，再根据∠C=∠ABC，即可判断出∠C=2∠D． 试题解析：∵AB=AC=AD， ∴∠C=∠ABC，∠D=∠ABD. ∴∠ABC=∠CBD＋∠D. ∵AD∥BC， ∴∠CBD=∠...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.2 用“角边角、角角边”判定三角形全等 同步练习 题型：解答题

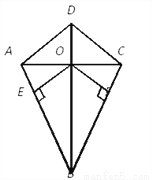
    我们把两组邻边相等的四边形叫做“筝形” .如图所示四边形ABCD是一个筝形，其中AB＝CB，AD＝CD，对角线AC，BD相交于点O，OE⊥AB，OF⊥CB，垂足分别是E，F.求证：OE＝OF.

    证明见解析. 【解析】试题分析：欲证明OE=OF，只需推知BD平分∠ABC，所以通过全等三角形△ABD≌△CBD（SSS）的对应角相等得到∠ABD=∠CBD，问题就迎刃而解了． 试题解析：证明：∵在△ABD和△CBD中， AB=CB，AD=BD，BD=BD， ∴△ABD≌△CBD（SSS）， ∴∠ABD=∠CBD， ∴BD平分∠ABC． 又∵OE⊥AB，O...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.2用关系式表示的变量间关系课时练习 题型：解答题

    为了解某种品牌小汽车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成下表：

    汽车行驶时间t（h）

    0

    1

    2

    3

    …

    油箱剩余油量Q（L）

    100

    94

    88

    82

    …

    ①根据上表的数据，请你写出Q与t的关系式；

    ②汽车行驶5h后，油箱中的剩余油量是多少？

    ③该品牌汽车的油箱加满50L，若以100km/h的速度匀速行驶，该车最多能行驶多远？

    ①Q=50﹣8t；②汽车行驶5h后，油箱中的剩余油量是10L；③该车最多能行驶625km. 【解析】试题分析：①由表格可知，开始油箱中的油为50L，每行驶1小时，油量减少8L，据此可得t与Q的关系式； ②求汽车行驶5h后，油箱中的剩余油量即是求当t=5时，Q的值； ③贮满50L汽油的汽车，理论上最多能行驶几小时即是求当Q=0时，t的值. 试题解析①Q与t的关系式为：Q=50...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.2用关系式表示的变量间关系课时练习 题型：单选题

    观察表格，则变量y与x的关系式为（　　）

    x

    1

    2

    3

    4

    …

    y

    3

    4

    5

    6

    …

    A. y=3x B. y=x+2 C. y=x﹣2 D. y=x+1

    B 【解析】观察图表可知，每对x，y的对应值，y比x大2， 故变量y与x之间的函数关系式：y=x+2． 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.2用关系式表示的变量间关系课时练习 题型：单选题

    某种签字笔的单价为2元，购买这种签字笔x支的总价为y元，则y与x之间的函数关系式为（ ）

    A. y=-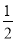x B. y=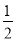x C. y=-2x D. y=2x

    D 【解析】依题意有：y=2x， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册达标检测 第二章 相交线与平行线 题型：解答题

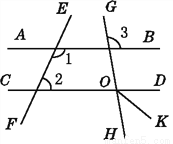
    如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH,求∠KOH的度数.

    40°. 【解析】根据平行线的判定、性质及角平分线的性质即可得到结果。

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册达标检测 第二章 相交线与平行线 题型：单选题

    ∠1和∠2是直线AB，CD被直线EF所截而形成的内错角，那么∠1和∠2的大小关系是( )

    A. ∠1=∠2 B. ∠1＞∠2 C. ∠1＜∠2 D. 无法确定

    D 【解析】【解析】 因为两直线的位置关系不确定，所以∠1和∠2的大小关系也无法确定．故选D．

    查看答案和解析>>

    科目：初中数学 来源：四川省实验学校2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    若a、b、c为整数，且|a﹣b|19+|c﹣a|95=1，则|c﹣a|+|a﹣b|+|b﹣c|=______．

    2 【解析】分两种情况： ①|a-b|=1，|c-a|=0，则c=a， ∴|c-a|+|a-b|+|b-c|=0+|a-b|+|b-a|=0+1+1=2； ②|a-b|=0，|c-a|=1，则a=b， |c-a|+|a-b|+|b-c|=|c-a|+0+|a-c|=1+0+1=2， ∴|c-a|+|a-b|+|b-c|=2. 故答案为：2．

    查看答案和解析>>

    同步练习册答案