
在Rt△ABC中,∠C=90°,sinA=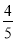 ,BC=20,则△ABC的面积为________.
,BC=20,则△ABC的面积为________.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:单选题
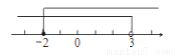
某不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
A. 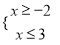 B.
B. 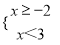 C.
C. 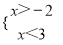 D.
D. 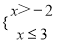
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:解答题
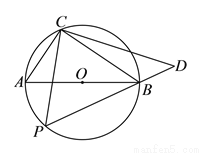
如图,圆 的直径为
的直径为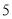 ,在圆
,在圆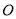 上位于直径
上位于直径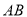 的异侧有定点
的异侧有定点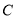 和动点
和动点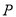 ,已知
,已知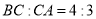 ,点
,点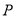 在半圆弧
在半圆弧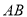 上运动(不与
上运动(不与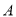 、
、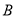 重合),过
重合),过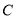 作
作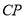 的垂线
的垂线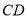 交
交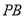 的延长线于
的延长线于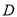 点.
点.
( )求证:
)求证: 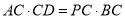 .
.
(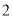 )当点
)当点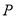 运动到
运动到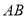 弧中点时,求
弧中点时,求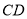 的长.
的长.
(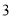 )当点
)当点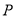 运动到什么位置时,
运动到什么位置时, 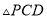 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积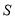 .
.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:单选题
如图,点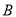 在线段
在线段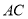 上,且
上,且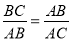 ,设
,设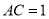 ,则
,则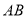 的长是( ).
的长是( ).
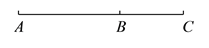
A. 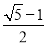 B.
B. 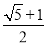 C.
C. 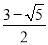 D.
D. 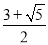
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:解答题
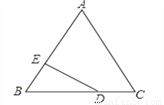
如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2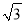 , 求AE.
, 求AE.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
△ABC中,∠C=90°,sinA=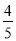 , 则tanA的值是( )
, 则tanA的值是( )
A. 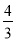 B.
B. 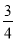 C.
C. 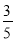 D.
D. 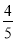
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
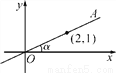
A. 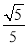 B.
B. 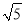 C.
C. 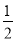 D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:填空题
如图,在矩形ABCD中,AB=6,AD=10,点E是边BC的中点,联结AE,若将△ABE沿AE翻折,点B落在点F处,联结FC,则cos∠ECF=________

查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册 同步测试 1.2 幂的乘法与积的乘方 题型:填空题
下列式子计算正确的是( )
A. x+x2=x3 B. 3x2﹣2x=x C. (3x2y)2=3x4y2 D. (﹣3x2y)2=9x4y2
D 【解析】试题解析:A. 不是同类项,不能合并,故错误. B. 不是同类项,不能合并,故错误. C. 故错误. D.正确. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com