
将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个;若这种商品的零售价在一定范围内每降价2元,其日销售量就增加4个,为了获得最大利润,则售价为________元,最大利润为________元.
90 800 【解析】设降价x元,利润为y, y=(100-70-x)(20+4×) =-2x2+40x+600 =-2(x-10)2+800, 当x=10时,y的最大值为800, 即售价为90元时,最大利润为800元. 故答案为90,800. 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
观察下列等式:
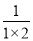 =1-
=1-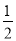 ,
, 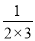 =
=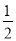 -
-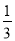 ,
, 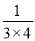 =
=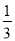 -
-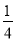 .
.
将以上三个等式的两边分别相加,得:
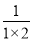 +
+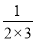 +
+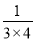 =1-
=1-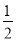 +
+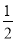 -
-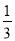 +
+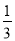 -
-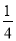 =1-
=1-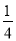 =
=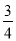 .
.
(1)直接写出计算结果:
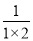 +
+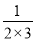 +
+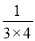 +…+
+…+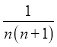 =________.
=________.
(2)仿照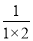 =1-
=1-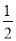 ,
, 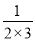 =
=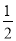 -
-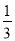 ,
, 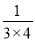 =
=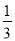 -
-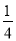 的形式,猜想并写出:
的形式,猜想并写出: 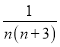 =________.
=________.
(3)解方程: 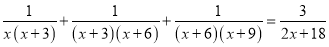 .
.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
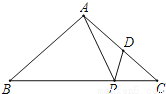
如图,已知: 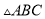 中,
中, 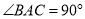 ,
, 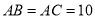 ,
, 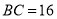 ,点
,点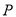 、
、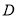 分别在边
分别在边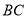 、
、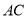 上,
上, 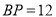 ,
, 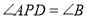 ,求
,求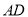 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
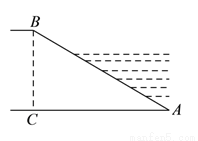
如图,河坝横断面迎水坡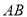 的坡比是
的坡比是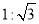 (坡比是坡面的铅直高度
(坡比是坡面的铅直高度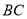 与水平宽度
与水平宽度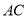 之比),坝高
之比),坝高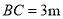 ,则坡面
,则坡面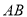 的长度是( ).
的长度是( ).
A. 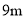 B.
B. 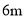 C.
C. 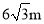 D.
D. 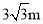
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
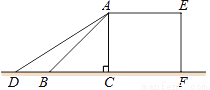
如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601, 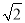 ≈1.414].
≈1.414].
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
在下列现象中:①时针转动,②电风扇叶片的转动,③转呼啦圈,④传送带上的电视机,其中是旋转的有( )
A. ①② B. ②③ C. ①④ D. ③④
A 【解析】、②属于旋转,③不止旋转,④是平移,不是旋转,所以是旋转的有①、②. 故选A.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
已知AB是⊙O的直径,弧AC的度数是30°.如果⊙O的直径为4,那么AC2等于( )
A. 2-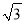 B. 4
B. 4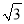 -6 C. 8-4
-6 C. 8-4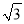 D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:填空题
使y=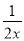 +x有意义的x的取值范围是_____.
+x有意义的x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20厘米,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3、6、9、12标在所在边的中点上,如图所示。
(1)问长方形的长应为多少?
(2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;
(3)请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、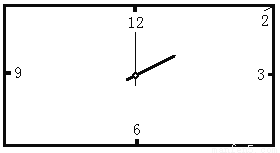
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com