
某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20厘米,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3、6、9、12标在所在边的中点上,如图所示。
(1)问长方形的长应为多少?
(2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;
(3)请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、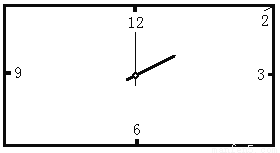
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个;若这种商品的零售价在一定范围内每降价2元,其日销售量就增加4个,为了获得最大利润,则售价为________元,最大利润为________元.
90 800 【解析】设降价x元,利润为y, y=(100-70-x)(20+4×) =-2x2+40x+600 =-2(x-10)2+800, 当x=10时,y的最大值为800, 即售价为90元时,最大利润为800元. 故答案为90,800.查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:解答题
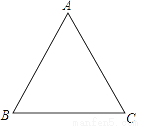
已知:在△ABC中,AB=AC,∠A=60°,求:∠B、∠C的度数,△ABC是什么三角形?
查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:填空题
已知 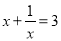 ,则代数式
,则代数式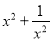 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
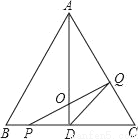
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D.点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)当x= 时,PQ⊥AC,x= 时,PQ⊥AB;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式为 ;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:填空题
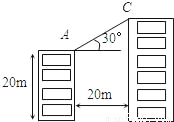
如图,甲、乙两楼相距20m,甲楼高20m,自甲楼顶A看乙楼楼顶C,仰角为30°,则乙楼的高为_____.(结果可用根式表示)
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
不等式组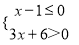 的解集为( )
的解集为( )
A. x≤1 B. x>﹣2 C. ﹣2<x≤1 D. 无解
C 【解析】试题解析: 解不等式①得,x≤1, 解不等式②得,x>-2, 所以不等式组的解集为:﹣2<x≤1. 故选C.查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
【答案】12
【解析】试题解析:设口袋中白球可能有x个,
∵摸到红球的频率稳定在40%附近,
∴口袋中摸到红色球的概率为40%,
∴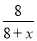 =40%,
=40%,
解得:x=12,
故答案为12.
【题型】填空题
【结束】
16
在等腰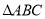 中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即
中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即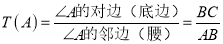 .例:T(60
.例:T(60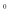 )=1,那么T(120
)=1,那么T(120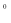 )=____________ ;
)=____________ ;
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
下列式子中,正确的是( )
A. a5n÷an=a5 B. (﹣a2)3•a6=a12 C. a8n•a8n=2a8n D. (﹣m)(﹣m)4=﹣m5
D 【解析】试题解析:A. a5n÷an=a5 ,错误; B. (﹣a2)3•a6=a12,错误; C. a8n•a8n=2a8n,错误; D. (﹣m)(﹣m)4=﹣m5,正确. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com