
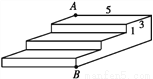
如图是一个三级台阶,它的每一级的长、宽和高分别等于5 cm,3 cm和1 cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源:黑龙江省安达市2017-2018学年七年级上学期期末质量检测数学试卷 题型:解答题
x2﹣12x+27=0.
x1=3,x2=9. 【解析】试题分析:将方程的左边因式分解,将一元二次方程转化为两个一元一次方程,即可解决问题. 试题解析:(x﹣3)(x﹣9)=0, x﹣3=0或x﹣9=0, 所以x1=3,x2=9.查看答案和解析>>
科目:初中数学 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:单选题
已知矩形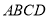 的对角线
的对角线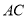 与
与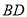 相交于点
相交于点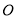 ,如果
,如果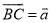 ,
, 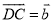 ,那么
,那么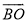 等于( )
等于( )
A. 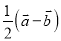 ; B.
; B. 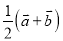 ; C.
; C. 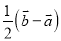 ; D.
; D. 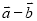 .
.
查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:单选题
用“整体法”求得方程(2x+5)2-4(2x+5)+3=0的解为( )
A. x1=1 x2=3 B. x1=-2 x2=3 C. x1=-3 x2=-1 D. x1=-2 x2=-1
D 【解析】【解析】 (2x+5)2﹣4(2x+5)+3=0,设2x+5=y,则原方程变形为y2﹣4y+3=0,解得:y1=1,y2=3,当y=1时,2x+5=1,解得:x=﹣2,当y=3时,2x+5=3,解得:x=﹣1,即原方程的解为x1=﹣2,x2=﹣1,故选D.查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:单选题
用配方法解方程 x2-2x-7=0 时,原方程应变形为( )
A. (x+1)2=8 B. (x+2)2=4 C. (x-1)2=8 D. (x-2)2=4
C 【解析】【解析】 方程x2﹣2x﹣7=0,变形得:x2﹣2x=7,配方得:x2﹣2x+1=8,即(x﹣1)2=8,故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:填空题
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 尺.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:单选题
如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
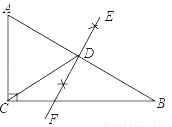
A. 13 B. 17 C. 18 D. 25
C 【解析】在Rt△ABC中,∠ACB=90°,BC=12,AC=5,根据勾股定理求得AB=13.根据题意可知,EF为线段AB的垂直平分线,在Rt△ABC中,根据直角三角形斜边的中线等于斜边的一半可得CD=AD=AB,所以△ACD的周长为AC+CD+AD=AC+AB=5+13=18.故选C.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:填空题
如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为 ;若添加条件AC=EC,则可以用 公理(或定理)判定全等.

查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:填空题
如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别取一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为____________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com