
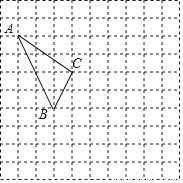
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标;
(4)求△ABC的面积.
科目:初中数学 来源:山东省2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
在矩形ABCD中,AD=5,AB=3,点E,F在直线AD上,且四边形BCFE为菱形,若线段EF的中点为点M,则线段AM的长为 .
6.5,或1.5. 【解析】 试题分析:两种情况:①由矩形的性质得出CD=AB=3,BC=AD=5,∠ADB=∠CDF=90°,由菱形的性质得出CF=EF=BE=BC=5,由勾股定理求出DF,得出MF,即可求出AM;②同①得出AE=4,求出ME,即可得出AM的长. 【解析】 分两种情况:①如图1所示: ∵四边形ABCD是矩形, ∴CD=AB=3,BC=AD=5,∠A...查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省诸城市 八年级上期末模拟数学试卷 题型:解答题
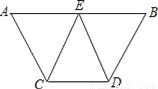
已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省诸城市 八年级上期末模拟数学试卷 题型:单选题
下列各式中,不能用平方差公式计算的是 ( )
A. (x+a)(a-x) B. (2-3x)(-2-3x)
C. (m+2n)(-m-2n) D. (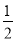 m-n)(n+0.5m)
m-n)(n+0.5m)
查看答案和解析>>
科目:初中数学 来源:山东省枣庄市滕州市2017-2018学年八年级(上)期中数学试卷 题型:填空题
规定用符号[m]表示一个实数m的整数部分,例如:[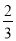 ]=0,[3.14]=3.按此规定[
]=0,[3.14]=3.按此规定[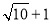 ]的值为_____.
]的值为_____.
查看答案和解析>>
科目:初中数学 来源:山东省枣庄市滕州市2017-2018学年八年级(上)期中数学试卷 题型:单选题
已知直线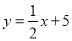 与一条经过原点的直线l平行,则这条直线l的函数关系式为( )
与一条经过原点的直线l平行,则这条直线l的函数关系式为( )
A. 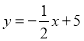 B.
B. 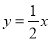 C.
C. 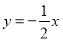 D. y=2x
D. y=2x
查看答案和解析>>
科目:初中数学 来源:北师大版数学八年级上册期末测评 题型:解答题
已知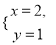 是二元一次方程组
是二元一次方程组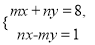 的解,求2m-n的算术平方根.
的解,求2m-n的算术平方根.
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级12月月考数学试卷 题型:单选题
如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于 ( )
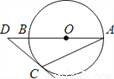
A. 20° B. 30° C. 40° D. 50°
C 【解析】如图,连接OC, ∵DC是⊙O的切线, ∴OC⊥DC, ∴∠OCD=90°. ∵OA=OC, ∴∠OCA=∠A=25°。 ∴∠DOC=∠OCA+∠A=50°, ∴∠D=180°-90°-50°=40°. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com