
不等式组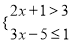 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A. 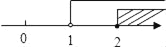 B.
B. 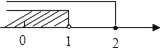
C. 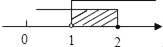 D.
D. 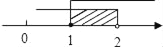
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
下列图形中,是中心对称图形的是( )
A.  B.
B. 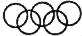 C.
C. 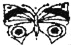 D.
D. 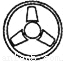
查看答案和解析>>
科目:初中数学 来源:广东省深圳市2017-2018北师大版八年级(上)数学期末模拟试卷 题型:填空题
已知直角三角形两边长分别为3cm,4cm,则第三条边长为_______________.
5 cm或cm 【解析】设第三边为xcm, (1)若4是直角边,则第三边x是斜边,由勾股定理得:32+42=x2,所以x=5; (2)若4是斜边,则第三边x为直角边,由勾股定理得:32+x2=42,所以x=; 综上第三边的长为5cm或cm, 故答案为:5cm或cm.查看答案和解析>>
科目:初中数学 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
先化简,再求代数式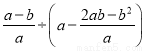 的值,其中
的值,其中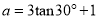 ,
, 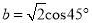 .
.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省武汉市中考数学模拟试卷 题型:单选题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).
其中正确的结论有( )
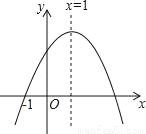
A. 2个 B. 3个 C. 4个 D. 5个
A 【解析】试题分析:根据图象可得:a<0,b>0,c>0,则abc<0,则①错误;当x=-1时,y<0,即a-b+c<0,则②错误;③、④、⑤正确.查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:解答题
若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.
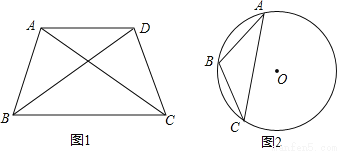
(1)如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数;
(2)如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹);
(3)在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.
(1)108°,72°,108°,72°. (2)图形见解析(3)∠BAD的度数为80°. 【解析】试题分析:(1)先由对角线AC是黄金线,可知△ABC是等腰三角形,分两种情况讨论:①AB=BC;②AC=BC.根据黄金四边形的定义和四边形的内角和求解即可; (2)①以A为圆心,AC为半径画弧,交圆O于D1,②以C为圆心,AC为半径画弧,交圆O于D2,③连接AD1,CD1,AD2,CD2...查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:填空题
如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:
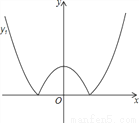
①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m<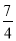 ;
;
③当m=-b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为 ______ .
②④ 【解析】试题分析:(1)当m=1,且y1与y2恰好有三个交点时,b有唯一值为1,b=,故(1)错误; (2)当b=2,且y1与y2恰有两个交点时,m>4或0<m<,故(2)正确; (3)当m=-b时,y1与y2没有交点,故(3)错误; (4)当m=b时,y1与y2至少有2个交点,且其中一个为(0,m)故(4)正确; 故答案为:(2),(3).查看答案和解析>>
科目:初中数学 来源:四川省西昌市航天学校2017-2018学年七年级上册数学期中测试卷(含答案) 题型:解答题
是否存在整数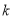 ,使关于
,使关于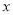 的方程
的方程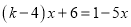 有整数解?若存在,请求出
有整数解?若存在,请求出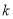 的值,并求出此方程的解;若不存在,请说明理由.
的值,并求出此方程的解;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷(B卷) 题型:单选题
北京时间上午8:30时,时钟上时针和分针之间的夹角(小于平角)是( )
A. 85° B. 75° C. 70° D. 60°
B 【解析】在钟面上,被12小时划分为12大格,每1大格对应的度数是30度,上午8:30的时候,时针指向8时和9时的中间位置,分针指向6时,两针之间刚好间隔2.5格, ∴8:30时,时针和分针之间的夹角为:30°2.5=75°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com