
若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.
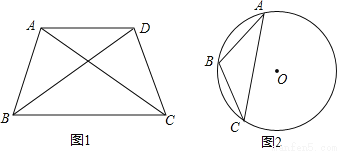
(1)如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数;
(2)如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹);
(3)在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.
(1)108°,72°,108°,72°. (2)图形见解析(3)∠BAD的度数为80°. 【解析】试题分析:(1)先由对角线AC是黄金线,可知△ABC是等腰三角形,分两种情况讨论:①AB=BC;②AC=BC.根据黄金四边形的定义和四边形的内角和求解即可; (2)①以A为圆心,AC为半径画弧,交圆O于D1,②以C为圆心,AC为半径画弧,交圆O于D2,③连接AD1,CD1,AD2,CD2... 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且?BCP=?ACD。
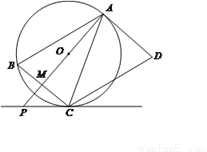
(1) 判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
(1)相切;证明见解析;(2). 【解析】试题分析:(1)通过分析,直线与圆O已经有一个公共点,连接半径0C,只要证明OC⊥PC即可;(2)根据AD是切线和AD∥BC证明AP⊥BC,利用垂径定理计算出CM=BM=3,在Rt△AMB中,利用勾股定义计算出AM的长,在Rt△OMC中,利用勾股定理建立方程计算出圆O的半径的长,最后证明△OMC~△OCP,利用相似三角形的对应边成比例计算出PC的长....查看答案和解析>>
科目:初中数学 来源:广东省深圳市2017-2018北师大版八年级(上)数学期末模拟试卷 题型:单选题
在平面直角坐标系中,点M(-3,2)向右平移2个单位,向下平移3个单位后得点N,则点N的坐标是( )
A. (1,1) B. (-1,1) C. (-1,-1) D. (1,-1)
C 【解析】点M(-3,2)向右平移2个单位后的坐标为(-1,2),再向下平移3个单位后的坐标为(-1,-1),即点N坐标为(-1,-1), 故选C.查看答案和解析>>
科目:初中数学 来源:2017年湖北省武汉市中考数学模拟试卷 题型:填空题
分解因式:9x2﹣6x+1= .
(3x﹣1)2 【解析】利用完全平方公式因式分解,得9x2﹣6x+1= . 故答案为(3x﹣1)2.查看答案和解析>>
科目:初中数学 来源:2017年湖北省武汉市中考数学模拟试卷 题型:单选题
不等式组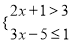 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A. 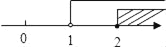 B.
B. 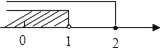
C. 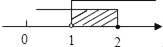 D.
D. 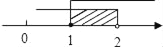
查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:解答题
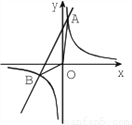
如图,已知反比例函数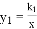 与一次函数
与一次函数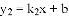 的图象交于点A(1,8),B(-4,m)两点.
的图象交于点A(1,8),B(-4,m)两点.
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式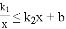 的解。
的解。
查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:填空题
分解因式:2x2﹣8x+8=_____.
2(x﹣2)2 【解析】试题解析:原式=2(x2-4x+4) =2(x-2)2.查看答案和解析>>
科目:初中数学 来源:四川省西昌市航天学校2017-2018学年七年级上册数学期中测试卷(含答案) 题型:解答题
(1)比较下列各式的大小:
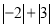
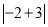 ;
;
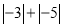
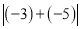 ;
;
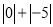
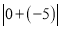 ;…
;…
(2)通过(1)的比较,请你分析,归纳出当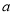 ,
, 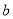 为有理数时,
为有理数时, 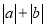 与
与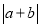 的大小关系.
的大小关系.
(3)根据(2)中你得出的结论,求当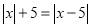 时,
时, 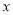 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷(B卷) 题型:单选题
小明做了以下4道计算题:①(-1)2008=2008;②0-(-1)=1;③- 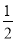 +
+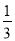 =-
=-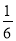 ;④
;④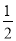 ÷(-
÷(-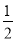 )=-1.请你帮他检查一下,他一共做对了( )
)=-1.请你帮他检查一下,他一共做对了( )
A. 1题 B. 2题 C. 3题 D. 4题
C 【解析】(1)因为,所以①错误; (2)因为,所以②正确; (3)因为,所以③正确; (4)因为,所以④正确; 综上所述,错误的1道,正确的3道. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com