练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知乘法公式：①(a＋b)(a4－a3b＋a2b2－ab3＋b4)＝a5＋b5；②(a－b)(a4＋a3b＋a2b2＋ab3＋b4)＝a5－b5利用上述公式对多项式x8＋x6＋x4＋x2＋1进行因式分解．

    答案：
    解析：

    　　解：由公式②知：

    　　x10－1＝(x2)5－1＝(x2－1)(x8＋x6＋x4＋x2＋1)

    　　∴x8＋x6＋x4＋x2＋1＝＝·＝(x4－x3＋x2－x＋1)(x4＋x3＋x2＋x＋1)

    　　分析：把待分解的多项式与所给公式比较，会发现待分解的多项式与公式②中的因式a4＋a3b＋a2b2＋ab3＋b4结构相似，事实上，只要令a＝x2，b＝1，则a4＋a3b＋a2b2＋ab3＋b4即x8＋x6＋x4＋x2＋1．

    　　点拨：若本题不能充分利用公式，要想对所给的多项式进行因式分解，很难很难，我们利用了因式分解与多项式的乘法是互为逆变形来解决问题，这也培养了我们的逆向思维能力．本题的创新之处就是利用所给的公式进行因式分解．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读并解答下列问题：我们熟悉两个乘法公式：①（a+b）2=a2+2ab+b2；②（a-b）2=a2-2ab+b2．现将这两个公式变形，可得到一个新的公式③：ab=（
    a+b
    2
    ）2-（
    a-b
    2
    ）2，这个公式形似平方差公式，我们不妨称之为广义的平立差公式．灵活、恰当地运用公式③将会使一些数学问题迎刃而解．
    例如：因式分解：（ab-1）2+（a+b-2）（ a+b-2ab）
    解：原式=（ab-1）2+[
    (a+b-2)-(a+b-2ab)
    2
    ]2    -[
    (a+b-2)-(a+b-2ab)
    2
    ]2
    =（ab-1）2+（a+b-ab-1）2-（ab-1）2=（a-1）（b-1）2=（a-1）2（b-1）2
    你能利用公式（或其他方法）解决下列问题吗？
    已知各实数a，b，c满足ab=c2+9且a=6-b，求证：a=b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•随州）在一次数学活动课上，老师出了一道题：
    （1）解方程x2-2x-3=0
    巡视后，老师发现同学们解此道题的方法有公式法、配方法和十字相乘法（分解因式法）．接着，老师请大家用自己熟悉的方法解第二道题：
    （2）解关于x的方程mx2+（m-3）x-3=0（m为常数，且m≠0）．
    老师继续巡视，及时观察、点拨大家，再接着，老师将第二道题变式为第三道题：
    （3）已知关于x的函数y=mx2+（m-3）x-3（m为常数）
    ①求证：不论m为何值，此函数的图象恒过x轴、y轴上的两个定点（设x轴上的定点为A，y轴上的定点为C）；
    ②若m≠0时，设此函数的图象与x轴的另一个交点为B．当△ABC为锐角三角形时，观察图象，直接写出m的取值范围．
    请你也用自己熟悉的方法解上述三道题．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年浙江省九年级数学竞赛模拟试卷一（解析版） 题型：解答题

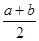    阅读并解答下列问题：我们熟悉两个乘法公式：①（+b）2=2+2b+b2;②(-b)2=2-2b+b2.现将这两个公式变形，可得到一个新的公式③：b=()2-(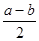)2, 这个公式形似平方差公式，我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。

    例如：因式分解：（b-1）2+(+b-2)( +b-2b)

    解：原式=+-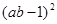

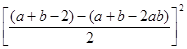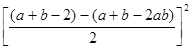
    =(b-1)2+(+b-b-1)2-(b-1)2=(-1)(b-1)2=（-1）2(b-1)2你能利用公式（或其他方法）解决下列问题吗？

    已知各实数，b，c满足b=c2+9且=6-b，求证：="b"

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知乘法公式：a5+b5=（a+b）（a4-a3b+a2b2-ab3+b4）；a5-b5=（a-b）（a4+a3b+a2b2+ab3+b4）．利用或者不利用上述公式，分解因式：x8+x6+x4+x2+1

    查看答案和解析>>

    同步练习册答案