
 如图,四边形ABCE中,AB=BC,AB⊥BC,CE⊥AE,BD⊥AE于D,求证:BD-CE=AD.
如图,四边形ABCE中,AB=BC,AB⊥BC,CE⊥AE,BD⊥AE于D,求证:BD-CE=AD. 证明:过C作CF⊥BD于F,则∠DBC+∠BCF=90°,
证明:过C作CF⊥BD于F,则∠DBC+∠BCF=90°, ,
,

科目:初中数学 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:047
请看下列例题及解答:
[例]如图,四边形ABCD中,AB∥CD,AD=DC=DB=6.5,BC=5,求对角线AC的长.
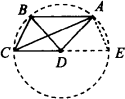
解答:以D为圆心,AD的长为半径作⊙D.显然⊙D经过点A、B、C.延长CD交⊙D于点E,连结AE,根据本节《探究体验》可知四边形ABCE为等腰梯形,故AE=BC=5.
∵CE为⊙D直径,∴∠CAE=90°.
在Rt△ACE中,CE=2AD=13,AE=5.
∴AC=![]() =12.
=12.
请构造辅助圆解决下列问题:如图,在四边形ABCD中,AB=AC=AD,且∠DBC=2∠BDC.求证:∠DAB=3∠BAC.

查看答案和解析>>
科目:初中数学 来源:初中数学解题思路与方法 题型:047
已知如图,四边形ABCE中,AC为对角线,AD⊥BC于D,且AC2=AE2+EC2,BD=CE,AD=AE.求证:AB=AC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com