设方程mx2-(m-2)x+m-3=0有整数解,试确定整数m的值,并求出这时方程的所有整数解.
解:当m=0,则2x-3=0,此时方程无整数解;
当m≠0时,△=(m-2)
2-4m(m-3)=-3m
2+8m+4,
把它看作二次函数,二次项系数为负,方程-3m
2+8m+4有解,解为m=
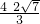
,
所以
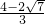
≤m≤
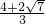
时,-3m
2+8m+4≥0,
因为m是整数,故只能取1,2,3.
当m=1时,方程x
2+x-2=0有解,解为-2和1;
当m=2时,方程2x
2-4=0无整数解:
当m=3时,方程3x
2-x=0有整数解:0.
所以当m=1时,方程x
2+x-2=0有解,整数解为-2和1;当m=3时,方程3x
2-x=0有整数解,整数解为0.
分析:先讨论m=0,方程无整数根;再讨论m≠0,首先确定原方程有根,得到m的范围,即△=(m-2)
2-4m(m-3)=-3m
2+8m+4≥0,利用二次函数的图象可求出m的范围,再根据m为整数,求出整数m,最后一一解方程得到满足条件的整数m.
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b
2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了运用二次函数解一元二次不等式和一元二次方程的解法.

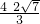 ,
,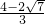 ≤m≤
≤m≤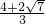 时,-3m2+8m+4≥0,
时,-3m2+8m+4≥0,

 (2012•随州)在一次数学活动课上,老师出了一道题:
(2012•随州)在一次数学活动课上,老师出了一道题: