
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
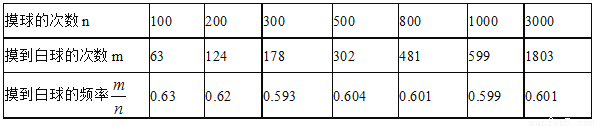
(1)请估计:当实验次数为5000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)试验估算这个不透明的盒子里黑球有多少只?
(1)接近 0.6 (2)0.6 (3)1 【解析】试题分析:(1)计算出其平均值即可; (2)概率接近于(1)得到的频率; (3)白球个数=球的总数×得到的白球的概率,让球的总数减去白球的个数即为黑球的个数. 【解析】 (1)∵摸到白球的频率为0.6, ∴当n很大时,摸到白球的频率将会接近0.6. (2)∵摸到白球的频率为0.6, ∴假如你摸一次,你摸...科目:初中数学 来源:2018人教版七年级数学下册练习:第七章达标检测卷 题型:填空题
在坐标系中,已知A(2,0),B(-3,-4),C(0,0),则△ABC的面积为( )
A. 4 B. 6 C. 8 D. 3
A 【解析】由题意点B坐标的纵坐标的绝对值即为△ABC底边AC的高, ∴AC=|2?0|=2, ∴S△ABC=×AC×|?4|=×2×4=4. 故选:A.查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
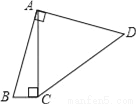
A. y=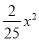 B. y=
B. y=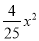 C. y=
C. y=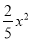 D. y=
D. y=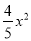
查看答案和解析>>
科目:初中数学 来源:河北省保定市莲池区2017-2018学年上期九年级数学期末考试试卷 题型:单选题
在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )
A. 35个 B. 30个 C. 20个 D. 15个
A 【解析】试题解析:设袋中有黄球x个,由题意得=0.3, 解得x=15,则白球可能有50-15=35个. 故选A.查看答案和解析>>
科目:初中数学 来源:河北省保定市莲池区2017-2018学年上期九年级数学期末考试试卷 题型:单选题
如图所示的几何体的俯视图是( )
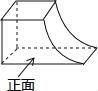
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:单选题
从长度分别为2、3、4、5的4条线段中任取3条,能构成钝角三角形的概率为( )
A. 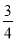 B.
B. 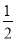 C.
C. 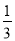 D.
D. 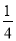
查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:单选题
下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是( ) 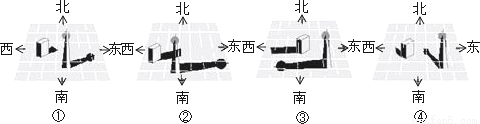
A. ③①④② B. ③②①④ C. ③④①② D. ②④①③
C 【解析】试题解析: 西为③,西北为④,东北为①,东为②, ∴将它们按时间先后顺序排列为③④①②. 故选:C.查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:单选题
若反比例函数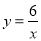 与一次函数
与一次函数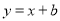 的图象交于点
的图象交于点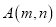 ,利用图象的对称性可知它们的另一个交点是
,利用图象的对称性可知它们的另一个交点是
A. 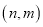 B.
B. 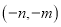 C.
C. 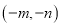 D.
D. 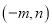
查看答案和解析>>
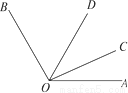
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年七年级上学期期末教学质量检测数学试卷 题型:解答题
如图,已知∠AOC:∠BOC=1:4,OD平分∠AOB,且∠COD=36°,求∠AOB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com