
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
下列命题其中真命题的个数是( )
(1)长度相等的弧是等弧;
(2)圆是轴对称图形,它的对称轴是过圆心的弦
(3)相等的圆心角所所对的弦相等;
(4)在同圆或者等圆中,相等的两弦所对的弧相等.
A. 0 B. 1 C. 2 D. 3
A 【解析】(1)在同圆或等圆中长度相等的弧是等弧,故(1)错误;(2)圆是轴对称图形,它的对称轴是过圆心的直线,故(2)错误;(3)在同圆或等圆中相等的圆心角所对的弦相等,故(3)错误;(4)在同圆或者等圆中,相等的两弦所对的优弧相等,劣弧相等,故(4)错误;所以真命题的个数是0, 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,DE∥BC,EF∥AB,且S△ADE=4,S△EFC=9,则△ABC的面积为
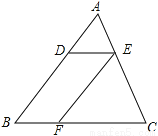
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=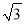 ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。

查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
2014年春节期间我市持续好天气,监测数据显示,1月30日至2月6日期间,我市空气质量均为良,空气污染指数如下表:
日期 | 30日 | 31日 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 |
污染指数 | 91 | 96 | 82 | 85 | 80 | 56 | 72 | 62 |
则这组数据的中位数和平均数分别为_____.
81,78 【解析】这组数据按照从小到大的顺序排列为:56,62,72,80,82,85,91,96, ∴这组数据的中位数为: , 平均数为: . 故答案为:81,78.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:单选题
如图,AB与⊙O相切于点B,AC的延长线交⊙O于点C连结BC若∠A=36°,则∠C等于( )
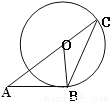
A. 36° B. 54° C. 60° D. 27°
D 【解析】试题分析:根据题目条件易求∠BOA,根据圆周角定理求出∠C=∠BOA,即可求出答案. ∵AB与⊙O相切于点B, ∴∠ABO=90°, ∵∠A=36°, ∴∠BOA=54°, ∴由圆周角定理得:∠C=∠BOA=27°, 故选D.查看答案和解析>>
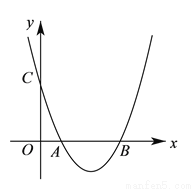
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:解答题
已知二次函数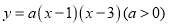 的图象与
的图象与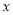 轴交于
轴交于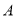 、
、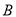 两点(
两点(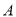 左
左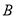 右),与
右),与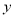 轴交于
轴交于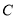 点
点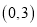 .
.
(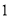 )求
)求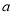 的值.
的值.
(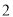 )若
)若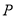 为二次函数
为二次函数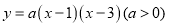 图象的顶点,求证:
图象的顶点,求证: 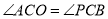 .
.
(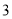 )若
)若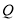 为二次函数
为二次函数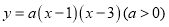 图象上一点,且
图象上一点,且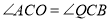 ,求
,求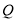 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:单选题
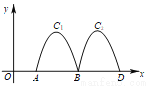
如图,抛物线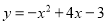 与
与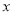 轴交于点
轴交于点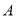 、
、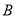 ,把抛物线在
,把抛物线在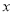 轴及其上方的部分记作
轴及其上方的部分记作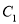 ,将
,将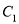 向右平移得
向右平移得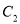 ,
, 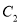 与
与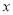 轴交于点
轴交于点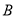 ,
, 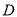 .若直线
.若直线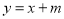 与
与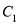 、
、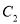 共有
共有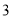 个不同的交点,则
个不同的交点,则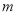 的取值范围是( ).
的取值范围是( ).
A. 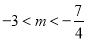 B.
B. 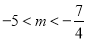 C.
C. 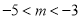 D.
D. 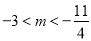
查看答案和解析>>
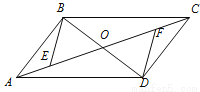
科目:初中数学 来源:2017年江苏省徐州市中考数学模拟试卷(2) 题型:解答题
如图,□ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com