练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

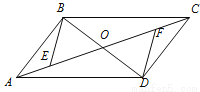
    如图，□ABCD的对角线AC、BD相交于点O，AE＝CF．

    （1）求证：△BOE≌△DOF；

    （2）若BD＝EF，连接DE、BF，判断四边形EBFD的形状，并说明理由．

    （1）证明见解析；（2）四边形EBFD为矩形，理由见解析． 【解析】试题分析：（1）先证出OE=OF，再由SAS即可证明△BOE≌△DOF； （2）由对角线互相平分证出四边形EBFD是平行四边形，再由对角线相等，即可得出四边形EBFD是矩形． 试题解析：（1）证明：∵四边形ABCD为平行四边形， ∴BO＝DO，AO＝CO． ∵AE＝CF， ∴AO－AE＝CO－C...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：填空题

    函数中自变量的取值范围是______.

    【解析】试题解析：根据题意得： 解得： .

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古乌兰察布市中考数学一模试卷 题型：解答题

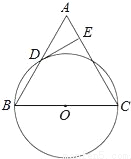
    已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

    （1）求证：点D是AB的中点；

    （2）判断DE与⊙O的位置关系，并证明你的结论；

    （3）若⊙O的直径为18，cosB=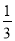，求DE的长．

    （1）证明见解析；（2）DE是⊙O的切线，证明见解析；（3）DE= ． 【解析】（1）证明：连接AD ∵AB为半圆O的直径, ∴AD⊥BC ∵AB=AC ∴点D是BC的中点 (2)【解析】 相切 连接OD ∵BD=CD，OA=OB， ∴OD∥AC ∵DE⊥AC ∴DE⊥OD ∴DE与⊙O相切 （3） ∵AB为半圆O的直...

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古乌兰察布市中考数学一模试卷 题型：单选题

    将一个半径为R，圆心角为90°的扇形围成一个圆锥的侧面（无重叠），设圆锥底面半径为r，则R与r的关系正确的是（　　）

    A. R=8r B. R=6r C. R=4r D. R=2r

    C 【解析】试题解析：根据扇形的弧长等于圆锥的底面周长，则 扇形的弧长是： 即 ∴R=4r. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学模拟试卷（2） 题型：解答题

    （14分）如图，在平面直角坐标系中，抛物线y=mx2﹣8mx+4m+2（m＞2）与y轴的交点为A，与x轴的交点分别为B（x1，0），C（x2，0），且x2﹣x1=4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q．

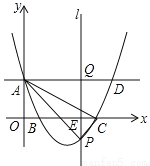
    （1）求抛物线的解析式；

    （2）当0＜t≤8时，求△APC面积的最大值；

    （3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，求出此时t的值；若不存在，请说明理由．

    （1）；（2）12；（3）t=或t=或t=14． 【解析】试题分析：（1）首先利用根与系数的关系得出： ，结合条件求出的值，然后把点B，C的坐标代入解析式计算即可；（2）（2）分0＜t＜6时和6≤t≤8时两种情况进行讨论，据此即可求出三角形的最大值；（3）（3）分2＜t≤6时和t＞6时两种情况进行讨论，再根据三角形相似的条件，即可得解． 试题解析：【解析】 （1）由题意知x1、x2是...

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学模拟试卷（2） 题型：填空题

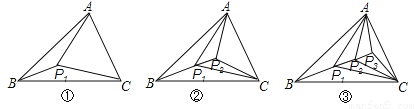
    如图，△ABC的三个顶点和它内部的点P1，把△ABC分成3个互不重叠的小三角形；△ABC的三个顶点和它内部的点P1、P2，把△ABC分成5个互不重叠的小三角形；△ABC的三个顶点和它内部的点P1、P2、P3，把△ABC分成7个互不重叠的小三角形；……，△ABC的三个顶点和它内部的点P1、P2、P3……Pn，把△ABC分成 个互不重叠的小三角形．

    3+2（n﹣1） 【解析】试题分析：由题及图象可知，当三角形内部有一个点时有3个三角形，以后三角形内部每增加一个点，就 会多两个三角形，所以当内部有n个点时共有3+2（n-1）=2n+1个互补重叠的三角形

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学模拟试卷（2） 题型：填空题

    若点A（3，-4）、B（-2，，m）在同一个反比例函数的图象上，则m的值为 。

    6 【解析】试题分析：将点A(3，－4)代入反比例函数可得函数解析式为：y=－；将点B(－2，m)代入反比例函数解析式可得：m=6.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型：解答题

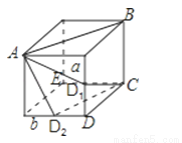
    如图，

    （1）一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B，怎样爬行路线最短？

    （2）如果要爬行到顶点C呢？说出你的理由．

    （1）沿线段AB爬行；（2）答案见解析 【解析】（1）根据线段的性质：两点之间线段最短可得沿线段AB爬行路线最短； （2）根据线段的性质：两点之间线段最短，把正方体展开，直接连接A、C两点可得最短路线． 【解析】 （1）沿线段AB爬行． （2）如果要爬行到顶点C，有三种情况：若蚂蚁爬行时经过面AD，可将这个正方体展开，在展开图上连接AC，与棱a（或b）交于点D1（或D2）...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（十） 题型：单选题

    如图，P为平行四边形ABCD边AD上一点，E、F分别为PB、PC的中点，△PEF、△PDC、△PAB的面积分别为S、S1、S2，若S=2，则S1+S2=（　　）

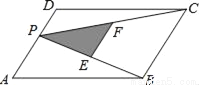
    A. 4 B. 6 C. 8 D. 不能确定

    C 【解析】试题分析：过P作PQ∥DC交BC于点Q，由DC∥AB，得到PQ∥AB， ∴四边形PQCD与四边形APQB都为平行四边形， ∴△PDC≌△CQP，△ABP≌△QPB， ∴S△PDC=S△CQP，S△ABP=S△QPB， ∵EF为△PCB的中位线， ∴EF∥BC，EF=BC， ∴△PEF∽△PBC，且相似比为1：2， ∴S△PEF：S△PBC...

    查看答案和解析>>

    同步练习册答案