
一元二次方程(1﹣k)x2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是_____.
k<2且k≠1 【解析】试题解析:∵a=1?k,b=?2,c=?1,一元二次方程有两个不相等的实数根, 解得k<2, ∵(1?k)是二次项系数,不能为0, ∴k≠1且k<2. 故答案为:k<2且k≠1. 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
如果两个角互补,则( )
A. 这两个角都是锐角 B. 这两个角都是钝角
C. 这两个角一个是钝角一个是锐角 D. 以上说法都是不正确
D 【解析】因为互补的两个角的和等于180°,所以互补的两个角可能是一个锐角,一个钝角;或两个都是直角. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:填空题
计算:(﹣2)0+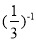 ﹣
﹣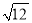 +2tan30°=_____.
+2tan30°=_____.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
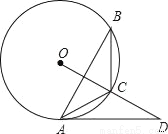
如图,△ABC内接于⊙O,过点A作⊙O的切线,交OC的延长线于点D,∠D=30°
(1)求∠B的度数;
(2)若OD⊥AB,BC=5,求AD的长.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:填空题
某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打_____折.
7 【解析】试题分析:设打x折,利用销售价减进价等于利润得到1200•﹣800≥800×5%,然后解不等式求出x的范围,从而得到x的最小值即可. 【解析】 设打x折, 根据题意得1200•﹣800≥800×5%, 解得x≥7. 所以最低可打七折. 故答案为七.查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:单选题
在Rt△ABC中,∠C=90°,AB=10,AC=6,则cosA的值等于( )
A. 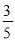 B.
B. 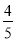 C.
C. 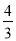 D.
D. 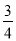
查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
为了落实国务院的指示精神,政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣x+60.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售的最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不能高于每千克35元,该农户想要每天获得300元的销售利润,销售价应定为每千克多少元?
(1)w=﹣x2+80x﹣1200;(2)答:该产品销售价定为每千克40元时,每天销售利润最大,最大销售利润400元.(3)该农户想要每天获得300元的销售利润,销售价应定为每千克30元. 【解析】试题分析:依据“利润=售价﹣进价”可以求得y与x之间的函数关系式,然后利用函数的增减性确定“最大利润”. 【解析】 (1)y=(x﹣20)w =(x﹣20)(﹣2x+80) =...查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:单选题
二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过( )
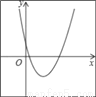
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
C 【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型:填空题
若|-a|=8,则a=______.
±8 【解析】∵|-a|=8, ∴|a|=8, ∴a=±8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com