
如图,已知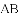
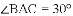
(1)求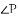
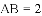
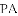
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:填空题
M为矩形ABCD的BC上一点,DN⊥AM于N,AB=3,BC=7,AM=5,则DN=______.
【解析】∵四边形ABCD是矩形,∴AD=BC=7,∠B=90°,AD//BC, ∴∠AMB=∠DAN, ∵∠AND=90°=∠B, ∴△ADN∽△MAB, ∴,即 ,∴DN= , 故答案为: .查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:填空题
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为________ m2 .
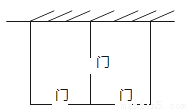
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 25.1.1随机事件 测试 题型:填空题
为了了解参加某运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄,“某运动员被抽到”这一事件是____事件,抽到的可能性为____.
随机 【解析】根据随机事件的性质可得,因为为了了解参加某运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄,所以在2000名运动员抽查100名运动员,所以这一事件为随机事件,且抽到的可能性为100÷2000=. 故答案为:随机, .查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:解答题
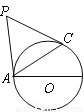
已知:如图,在 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
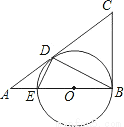
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
(1)证明见解析;(2)证明见解析. 【解析】 试题分析:从切线的性质出发,通过切线与弦所夹的角与弧弦夹角相等,即得到∠CDB=∠CBA;由切线的性质而求得. 试题解析:(1)证明:∵∠ABC=90°, ∴OB⊥BC ∵OB是⊙O的半径, ∴CB为⊙O的切线. 又∵CD切⊙O于点D, ∴BC=CD; (2)证明:∵BE是⊙O的直径, ∴∠...查看答案和解析>>
科目:初中数学 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:解答题
如图所示,DE⊥AC,BF⊥AC,垂足分别为E,F, DE=BF,AF=CE.求证:AB∥CD.
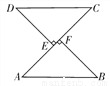
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:单选题
如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
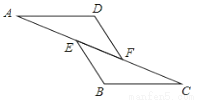
A. ∠A=∠C B. AD=CB C. BE=DF D. AD∥BC
B 【解析】试题分析:求出AF=CE,再根据全等三角形的判定定理判断即可.∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,A、∵在△ADF和△CBE中,∠A=∠C,AF=CE,∠AFD=∠CEB,∴△ADF≌△CBE(ASA),正确,故本选项错误;B、根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项正确;C、∵在△ADF和△CBE中,AF=CE,...查看答案和解析>>
科目:初中数学 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,△ABC的周长为19cm,AC的垂直平分线DE交AC于点E,E为垂足,AE=3cm,则△ABD的周长为________.
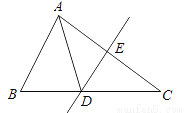
查看答案和解析>>
科目:初中数学 来源:2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型:解答题
某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费.如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式;
(2)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
(1)当x≤20时,y=1.9x、当x>20时,y=2.8x-18;(2)30吨. 【解析】 试题分析:本题分x≤20和x>20两种情况分别列出函数解析式;首先根据平均水费得出用水量的范围,然后代入函数解析式计算用水量. 试题解析:(1)当x≤20时,y=1.9x; 当x>20时,y=1.9×20+(x-20)×2.8=2.8x-18 . (2)因为5月份水费平均为每...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com