练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

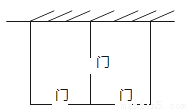
    某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，则能建成的饲养室面积最大为________ m2 ．

    75 【解析】试题分析：首先设垂直于墙面的长度为x，则根据题意可得：平行于墙面的长度为（30－3x），则S=x（30－3x）=－3+75，,则当x=5时，y有最大值，最大值为75，即饲养室的最大面积为75平方米.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷 题型：解答题

    先阅读，再因式分【解析】
    x4＋4＝(x4＋4x2＋4)－4x2＝(x2＋2)2－(2x)2＝(x2－2x＋2)(x2＋2x＋2)，按照这种方法把多项式x4＋324因式分解．

    (x2＋18＋6x)(x2＋18－6x)． 【解析】试题分析：仿照材料依据完全平方式的特点将x4＋324加上2×18x2使之成为完全平方式，再减去2×18x2，前三项利用完全平方公式分解，然后再与最后一项利用平方差公式分解即可． 试题解析： x4＋324 ＝x4＋36x2＋324－36x2 ＝(x2＋18)2－36x2 ＝(x2＋18)2－(6x)2 ＝(...

    查看答案和解析>>

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：单选题

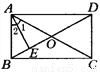
    如图所示，矩形ABCD的对角线交于O，AE⊥BD于E，∠1：∠2=2：1， 则∠1的度数为（ ）．

    A. 22．5° B. 45° C. 30° D. 60°

    B 【解析】∵四边形ABCD为矩形，AE⊥BD， ∴∠2+∠ABD=∠ADB+∠ABD =∠EAD+∠ADB=90°， ∴∠ADB=∠2，∠1+∠OAD+∠ADB=90°， ∵四边形ABCD是矩形，∴AO=OD，∴∠OAD=∠ADB=∠2，∴∠1+2∠2=90°， ∵∠1：∠2=2：1，∴2∠2=∠1， ∴2∠1=90°， ∴∠1=45°， 故选B....

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型：单选题

    如图，函数y=－a(x+a)与y=－ax2(a≠0)在同一坐标系上的图象是（）

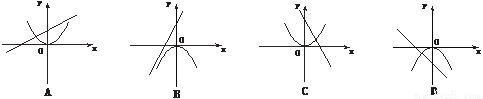
    A. A B. B C. C D. D

    D 【解析】A选项中，抛物线开口向上说明a<0，则一次函数y=－a(x+a)=-ax-a2应该与y轴交于负半轴，所以A不正确； B选项中，抛物线开口向下说明a>0，则一次函数y=－a(x+a)=-ax-a2的图象应该从左至右下降，所以B不正确； C选项中，抛物线开口向上说明a<0，则一次函数y=－a(x+a)=-ax-a2的图象应该从左至右上升，所以C不正确； D选项中，抛...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型：填空题

    若抛物线y=ax2经过点A (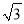，－9)，则其解析式为_______________。

    y=-3x2 【解析】把点A代入： 得， ，解得： ， ∴该抛物线的解析式为： .

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（1）练习 题型：填空题

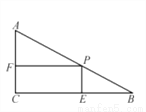
    如图，在Rt△ABC中，∠C=90°,∠B=30°,AB=12cm，点P是AB边上的一个动点，过点P作PE⊥BC于点E,PF⊥AC于点F,当PB=6cm时，四边形PECF的面积最大，最大值为______

    9cm2 【解析】试题分析：设PE=x，在Rt△PEB中，根据∠B=30°，可知PB=2x，BE=x，再在Rt△ABC中，利用三角函数的知识求出BC的长，进而可以表示出CE的长度；然后利用矩形的面积公式，即可得到四边形PECF的面积S关于x的表达式，对表达式进行配方，利用二次函数的最值即可得到答案. 【解析】 设PE=x，由∠B=30°， 得PB=2x，BE=x. 由AB...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（1）练习 题型：单选题

    用一条长为40cm的绳子围成一个面积为acm2的长方形，a的值不可能为

    A．20 B． 40 C．100 D．120

    D． 【解析】 试题分析：设围成面积为acm2的长方形的长为xcm，由长方形的周长公式得出宽为（40÷2-x）cm，根据长方形的面积公式列出方程x（40÷2-x）=a，整理得x2-20x+a=0，由△=400-4a≥0，求出a≤100，即可求解． 试题解析：设围成面积为acm2的长方形的长为xcm，则宽为（40÷2-x）cm，依题意，得 x（40÷2-x）=a，整理，得 ...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（3）练习 题型：解答题

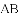
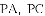
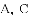
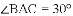
    如图，已知为⊙O 的直径，是⊙O 的切线，为切点，.

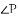
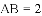
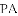
    （1）求的大小；（2）若，求的长（结果保留根号）．

    （1）60°；（2）. 【解析】试题分析：（Ⅰ）∵PA是⊙O的切线，AB为⊙O的直径， ∴PA⊥AB， ∴∠BAP=90°； ∵∠BAC=30°， ∴∠CAP=90°-∠BAC=60°． 又∵PA、PC切⊙O于点A、C， ∴PA=PC， ∴ △PAC为等边三角形， ∴∠P=60°． （Ⅱ）如图，连接BC，则∠ACB=90°． 在Rt...

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

    如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（　　）

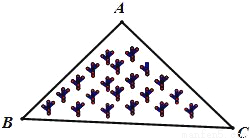
    A. △ABC的三条中线的交点 B. △ABC三边的中垂线的交点

    C. △ABC三条角平分线的交点 D. △ABC三条高所在直线的交点

    C 【解析】试题分析：要使点到角两边的距离则这个点在这个角的角平分线上.

    查看答案和解析>>

    同步练习册答案