
已知一元二次方程的两根分别是2和-3,则这个一元二次方程是( )
A. x2-6x+8=0 B. x2+2x-3=0 C. x2-x-6=0 D. x2+x-6=0
D 【解析】2-3=-1,2,利用韦达定理知, x2+x-6=0.所以选D.科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
下列二次根式中是最简二次根式的是( )
A. 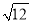 B.
B. 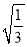 C.
C. 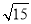 D.
D. 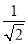
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
若关于x的方程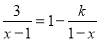 有增根,则k的值为( ).
有增根,则k的值为( ).
A. 3 B. 1 C. 0 D. -1
A 【解析】试题解析:首先根据解分式方程的方法求出x的值,然后根据增根为x=1代入方程求出k的值.将方程的两边同时乘以(x-1)可得:3=x-1+k,解得:x=4-k,根据方程有增根可得:x=1,即4-k=1,k=3.查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:解答题
已知关于x的一元二次方程x2﹣(k+2)x+2k=0.
(1)若x=1是这个方程的一个根,求k的值和它的另一根;
(2)对于任意的实数k,判断原方程根的情况,并说明理由.
(1)k=1;另一根为x=2;(2)证明见解析. 【解析】试题分析:(1)把x=1代入方程得到关于k的方程,求出k的值,再把k的值代入原方程,然后利用因式分解法解方程求出方程的另一根; (2)计算判别式得到△=(k+2)2﹣4×2k=k2﹣4k+4=(k﹣2)2 , 根据非负数的性质得到△≥0,然后根据判别式的意义判断方程根的情况. 试题解析:(1)∵x=1是方程x2﹣(k+2)...查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:填空题
小华与父母从合肥乘车去无为县米公祠(北宋大书法家米芾故居)参观,车厢里每排有左、中、右三个座位,小华一家三口随意坐某排的三个座位,则小华恰好坐在中间的概率是 .
. 【解析】 试题分析:共有三个座位,小华有三种坐法;小华恰好坐在中间是其中一种情况;故则小华恰好坐在中间的概率是. 故答案是.查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:单选题
下列命题中,正确命题的个数为( )
(1)三点确定一个圆 (2)平分弦的直径垂直于这条弦
(3)等弧对等弦 (4)直径是圆的对称轴
A.1 B.2 C.3 D.4
A 【解析】 试题分析:根据与圆有关的基本概念依次分析各小题即可作出判断. (1)不共线的三点确定一个圆,(2)在同圆中,平分弦的直径垂直于这条弦,(4)直径所再的直线是圆的对称轴,故错误; (3)等弧对等弦,正确; 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
数学课上老师提出了下面的问题:
在正方形ABCD对角线BD上取一点F,使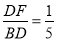 .小明的做法如下:如图,
.小明的做法如下:如图,
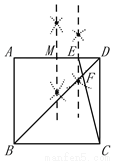
①应用尺规作图作出边AD的中点M;
②应用尺规作图作出MD的中点E;
连接EC,交BD于点F.
所以F点就是所求作的点.
请你判断小明的做法是否正确,并说明理由.
正确,理由见解析. 【解析】试题分析: 由作图易得,再证△DEF∽△BFC可得,由此即可得到,从而说明小明的做法正确. 试题解析: 小明的做法正确,理由如下: 由做法可知M为AD的中点,E为MD的中点, ∴, ∵四边形ABCD是正方形, ∴AD=BC,ED∥BC, ∴△DEF∽△BFC, ∴=, ∵AD=BC ∴==, ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:单选题
网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB的高度).中网比赛中,某运动员退出场地在距球网14米的D点处接球,设计打出直线穿越球,使球落在对方底线上C处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为( )

A. 1.65米 B. 1.75米 C. 1.85米 D. 1.95米
D 【解析】如图,由题意可知,AB∥DE, ∴△CBA∽△CDE, ∴, ∵AB=0.9,CB=12,CD=CB+BD=26, ∴, ∴12DE=0.9×26, ∴DE=1.95(米). 故选D.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷及答案 题型:解答题
先化简,再求值: 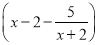 ?
?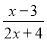 ,其中x=2.
,其中x=2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com