
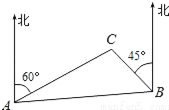
如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则从C点看A、B两岛的视角∠ACB=_____°.
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年七年级上学期期中联考数学试卷 题型:单选题
实数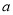 、
、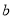 在数轴上的位置如图所示,下列结论正确的是 ( )
在数轴上的位置如图所示,下列结论正确的是 ( )

A. 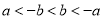 B.
B. 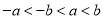
C. 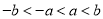 D.
D. 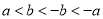
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:解答题
计算:
(1) 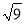 ﹣|-5|﹣(3-π)0+2014
﹣|-5|﹣(3-π)0+2014
(2) 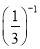 -|
-|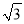 -3|-
-3|-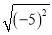
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:解答题
如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
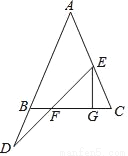
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:填空题
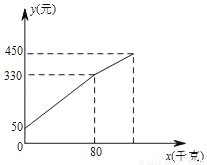
一水果商贩在批发市场按1.8元/千克批发了若干千克的苹果进城出售,为了方便,他带了一些零钱备用,他先按市场价出售一些后,又每千克下降0.5元将剩余的苹果降价售完,这时他手中的钱(含备用零钱)是450元.售出苹果x千克与他手中持有的钱数y元(含备用零钱)的关系如图所示,则这个水果商贩一共赚_____元.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:单选题
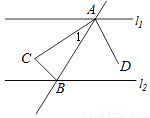
如图,已知l1∥l2 , AC、BC、AD为三条角平分线,则图中与∠1互为余角的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
D 【解析】因为l1∥l2 , AC,BC,AD为三条角平分线, 所以∠1+∠2=90°,所以∠1和∠2互余,又因为∠2=∠3,所以∠1+∠3=90°,所以∠1和∠3互余, 因为∠1+∠4=180°÷2=90°,所以∠1和∠4互余, 又因为∠4=∠5,所以∠1+∠5=90°,所以∠1和∠5互余, 所以∠1的余角有4个,故选D.查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:单选题
如图,点C在∠AOB的OB边上,用尺规作出了CN∥OA,作图痕迹中, 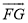 是( )
是( )
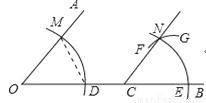
A. 以点C为圆心,OD为半径的弧 B. 以点C为圆心,DM为半径的弧
C. 以点E为圆心,OD为半径的弧 D. 以点E为圆心,DM为半径的弧
D 【解析】试题分析:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧. 故选D.查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:填空题
若一个正数的两个平方根是2a-1和-a+2,这个正数是____ .
9 【解析】试题分析:依题意得,2a-1+(-a+2)=0, 解得:a=-1. 则这个数是(2a-1)2=(-3)2=9. 故答案为:9.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:解答题
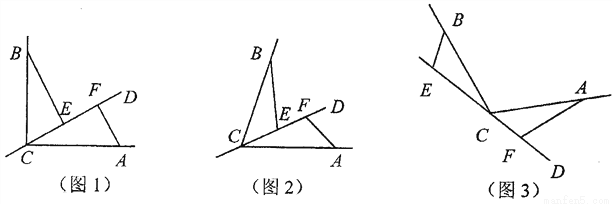
已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠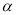 .
.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠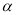 =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠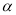 与∠BCA关系的条件___ ____使①中的结论仍然成立;
与∠BCA关系的条件___ ____使①中的结论仍然成立;
(2)如图3,若直线CD经过∠BCA的外部,∠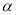 =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com