
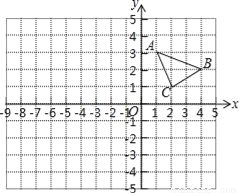
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)在图中以点O为位似中心在原点的另一侧画出△ABC放大2倍后得到的△A1B1C1,并写出A1的坐标;
(2)请在图中画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:甘肃省定西市安定区2016-2017学年八年级上学期期末考试数学试卷 题型:解答题
化简:
(1)(-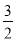 ab-2a)(-
ab-2a)(-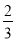 a2b2);
a2b2);
(2)(2m-1)(3m-2).
(1) a3b3+a3b2;(2) 6m2-7m+2. 【解析】试题分析:(1)根据单项式乘以多项式的运算法则进行计算即可求得结果; (2)根据多项式乘以多项式的运算法则进行计算即可求得结果. 试题解析:(1)原式=a3b3+a3b2; (2)原式=6m2-4m-3m+2 =6m2-7m+2.查看答案和解析>>
科目:初中数学 来源:广西崇左市天等县2017年中考数学一模试卷 题型:解答题
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).
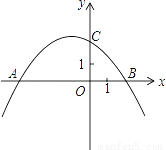
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.
(1)y=﹣x2﹣x+2;(2)2,D的坐标为(﹣2,2);(3)y=x﹣或y=﹣x﹣. 【解析】试题分析: (1)由已知条件可设抛物线解析式为: ,再代入点C的坐标(0,2)解得的值即可得到抛物线的解析式; (2)如图2,过点D作DH⊥AB于H,交直线AC于点G,由A、C的坐标求出直线AC的解析式,设点D的横坐标为“m”,则可用含“m”的代数式表达出DG的长,结合S△ADC=D...查看答案和解析>>
科目:初中数学 来源:广西崇左市天等县2017年中考数学一模试卷 题型:单选题
若反比例函数y=  的图象经过点(2,3),则它的图象也一定经过的点是( )
的图象经过点(2,3),则它的图象也一定经过的点是( )
A. (﹣3,﹣2) B. (2,﹣3) C. (3,﹣2) D. (﹣2,3)
A 【解析】试题分析:根据题意得k=2×3=6,所以反比例函数解析式为y=,∵﹣3×(﹣2)=6,2×(﹣3)=﹣6,3×(﹣2)=﹣6,﹣2×3=﹣6,∴点(﹣3,﹣2)在反比例函数y=的图象上.故选A.查看答案和解析>>
科目:初中数学 来源:广西崇左市天等县2017年中考数学一模试卷 题型:单选题
实数0是( )
A. 有理数 B. 无理数 C. 正数 D. 负数
A 【解析】试题分析:根据实数的分类可知: 0是有理数, 故选:A查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期第三次月考数学试卷 题型:填空题
已知点(﹣1,y1),(2,y2),(3,y3)在反比例函数y=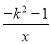 的图象上,则用“<”连接y1,y2,y3为_____.
的图象上,则用“<”连接y1,y2,y3为_____.
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期第三次月考数学试卷 题型:单选题
如图,在□ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
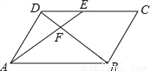
A. 3:2 B. 1:1 C. 2:5 D. 2:3
D 【解析】因为DE∥AB,所以△DEF∽△BAF,所以,则,所以. 故选D.查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:填空题
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D点,AB=4,BD=5,点P是线段BC上的一动点,则PD的最小值是________ .
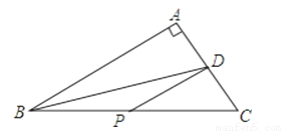
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
对于二次函数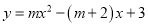 有下列说法:
有下列说法:
①如果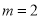 ,则
,则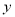 有最小值
有最小值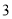 ;
;
②如果当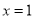 时的函数值与
时的函数值与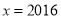 时的函数值相等,则当
时的函数值相等,则当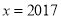 时的函数值为
时的函数值为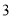 ;
;
③如果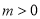 ,当
,当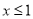 时
时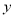 随
随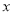 的增大而减小,则
的增大而减小,则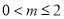 ;
;
④如果用该二次函数有最小值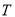 ,则
,则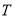 的最大值为
的最大值为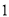 .
.
其中正确的说法是__________.(把你认为正确的结论的序号都填上)
②③④ 【解析】①时, ,即有最小值,故①错误. ②当时的函数时与时函数值相等时, 与时的函数值相等,且,故②正确. ③二次函数对称轴为直线, ∵时, 随的增大而减小,∴,∴,故③正确. ④二次函数恒定过点,∴,故④正确. 故答案为:②③④查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com